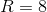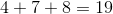All Common Core: 3rd Grade Math Resources
Example Questions
Example Question #1 : Solve Two Step Word Problems Using The Four Operations: Ccss.Math.Content.3.Oa.D.8
Jessica has been collecting beads all summer. She started with 


To solve this problem, we first have to find our unknowns. Our unknowns are the number of beads she will have by the end of the summer and the number of beads each of her friends will receive. We can set up equations for these unknowns by letting 





Example Question #1 : Solving Problems Involving The Four Operations, And Identifying And Explaining Patterns In Arithmetic
Emily has been collecting beads all summer. She started with 


To solve this problem, we first have to find our unknowns. Our unknowns are the number of beads she will have by the end of the summer and the number of beads each of her friends will receive. We can set up equations for these unknowns by letting 





Example Question #771 : Operations & Algebraic Thinking
Justin loves to run and is training for a marathon at the end of the month. His training program has him running 

To solve this problem, we first have to find our unknowns. Our unknowns are the number of miles he runs during the week and the total miles that he runs. We can set up equations for these unknowns by letting 






Example Question #4 : Solve Two Step Word Problems Using The Four Operations: Ccss.Math.Content.3.Oa.D.8
Jason loves to run and is training for a marathon at the end of the month. His training program has him running 

To solve this problem, we first have to find our unknowns. Our unknowns are the number of miles he runs during the week and the total miles that he runs. We can set up equations for these unknowns by letting 






Example Question #5 : Solve Two Step Word Problems Using The Four Operations: Ccss.Math.Content.3.Oa.D.8
Hannah is making a red fruit salad because red is her favorite color. She cuts up 

To solve this problem, we first have to find our unknowns. Our unknowns are the number strawberries and raspberries she puts in the fruit salad. We can set up equations for these unknowns by letting 




Now we need to add the watermelon, strawberries, and raspberries together to find our total.
Example Question #2 : Solve Two Step Word Problems Using The Four Operations: Ccss.Math.Content.3.Oa.D.8
Hannah is making a red fruit salad because red is her favorite color. She cuts up 

To solve this problem, we first have to find our unknowns. Our unknowns are the number strawberries and raspberries she puts in the fruit salad. We can set up equations for these unknowns by letting 




Now we need to add the watermelon, strawberries, and raspberries together to find our total.
Example Question #771 : Common Core Math: Grade 3
Ali is hanging up flyers around her school. She started with 

To solve this problem, we first have to find our unknowns. Our unknowns are the number of flyers that she hung on the west side of the building and the number of flyers she has left over. We can set up equations for these unknowns by letting 




To find the total number of flyers that she hung we add the amount of flyers on the east side and the amount on the west side.
To find how many flyers she has left, we subtract that total flyers that were hung from the 
Example Question #8 : Solve Two Step Word Problems Using The Four Operations: Ccss.Math.Content.3.Oa.D.8
Sara is hanging up flyers around her school. She started with 

To solve this problem, we first have to find our unknowns. Our unknowns are the number of flyers that she hung on the west side of the building and the number of flyers she has left over. We can set up equations for these unknowns by letting 




To find the total number of flyers that she hung we add the amount of flyers on the east side and the amount on the west side.
To find how many flyers she has left, we subtract that total flyers that were hung from the 
Example Question #772 : Operations & Algebraic Thinking
In Spot’s toy basket he has 

To solve this problem, we first have to find our unknowns. Our unknowns are the number of ropes and stuffed animals that Spot has. We can set up equations for these unknowns by letting 






Now we need to add up our number of balls, stuffed animals and ropes to find our total.
Example Question #773 : Operations & Algebraic Thinking
Charlie swims laps in the pool every day during the week before school. On Monday and Tuesday he swims 

To solve this problem, we first have to find our unknowns. Our unknowns are the number of laps he swims on Wednesday and Thursday and the number of laps he swims on Friday. We can set up equations for these unknowns by letting 





To find the total amount of laps that he swam, we need to add up the laps that he did each day.
Certified Tutor
All Common Core: 3rd Grade Math Resources