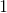All Common Core: 7th Grade Math Resources
Example Questions
Example Question #1 : Develop A Uniform Probability Model By Observing Frequencies In Data Generated From A Chance Process: Ccss.Math.Content.7.Sp.C.7b
Kelly spun a spinner, which is pictured below, 


The theoretical probability is what should happen. In this case, we have 


Example Question #2 : Finding Theoretical Probability
Kelly spun a spinner, which is pictured below, 


The theoretical probability is what should happen. In this case, we have 


Example Question #2 : Develop A Uniform Probability Model By Observing Frequencies In Data Generated From A Chance Process: Ccss.Math.Content.7.Sp.C.7b
Kelly spun a spinner, which is pictured below, 


The theoretical probability is what should happen. In this case, we have 


Example Question #993 : Grade 7
Kelly spun a spinner, which is pictured below, 


More likely
Less likely
Equally likely
Results can't be found based on the data provided
More likely
The theoretical probability is what should happen. In this case, we have 

The experimental probability is what actually happened in an experiment. In this case, Kelly spun the spinner 

In order to compare the theoretical probability and the experimental probability let's convert the fractions into decimals so we can put them on a number line:

A probability closer to 


Example Question #1 : Develop A Uniform Probability Model By Observing Frequencies In Data Generated From A Chance Process: Ccss.Math.Content.7.Sp.C.7b
Kelly spun a spinner, which is pictured below, 


Equally likely
Less likely
More likely
Results can't be found based on the data provided
More likely
The theoretical probability is what should happen. In this case, we have 


The experimental probability is what actually happened in an experiment. In this case, Kelly spun the spinner 

In order to compare the theoretical probability and the experimental probability let's convert the fractions into decimals so we can put them on a number line:

A probability closer to 


Example Question #2 : Develop A Uniform Probability Model By Observing Frequencies In Data Generated From A Chance Process: Ccss.Math.Content.7.Sp.C.7b
Kelly spun a spinner, which is pictured below, 


The theoretical probability is what should happen. In this case, we have 

All Common Core: 7th Grade Math Resources