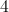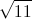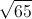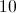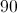Call Now to Set Up Tutoring:

(888) 888-0446

Common Core: 8th Grade Math : Apply the Pythagorean Theorem to Determine Unknown Side Lengths in Right Triangles: CCSS.Math.Content.8.G.B.7

Study concepts, example questions & explanations for Common Core: 8th Grade Math

Create An Account

All Common Core: 8th Grade Math Resources

7 Diagnostic Tests 75 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Apply The Pythagorean Theorem To Determine Unknown Side Lengths In Right Triangles: Ccss.Math.Content.8.G.B.7

The base and height of a right triangle are each 1 inch. What is the hypotenuse?

Possible Answers:

0.5

$\sqrt{2}$

Correct answer:

$\sqrt{2}$

Explanation:

You need to use the Pythagorean Theorem, which is $a^{2}+b^{^{2}} = c^{^{2}}$ .

Add the first two values and you get . Take the square root of both sides and you get $\sqrt{2}$ .

Report an Error

Example Question #2 : Apply The Pythagorean Theorem To Determine Unknown Side Lengths In Right Triangles: Ccss.Math.Content.8.G.B.7

A right triangle has legs with lengths of units and units. What is the length of the hypotenuse?

Possible Answers:

5.20 units

5.38 units

4.64 units

units

Correct answer:

5.38 units

Explanation:

$\text{Hypotenuse}=\sqrt{\text{(leg 1)}^2+\text{(leg 2)}^2}$

Using the numbers given to us by the question,

$\text{Hypotenuse}=\sqrt{2^2+5^2}=\sqrt{29}=5.38$ units

Report an Error

Example Question #3 : Apply The Pythagorean Theorem To Determine Unknown Side Lengths In Right Triangles: Ccss.Math.Content.8.G.B.7

A right triangle has legs with the lengths $4\:cm$ and $5\:cm$ . Find the length of the hypotenuse.

Possible Answers:

$3\:cm$

$41\:cm$

$\sqrt{35}\:cm$

$\sqrt{41}\:cm$

Correct answer:

$\sqrt{41}\:cm$

Explanation:

Use the Pythagorean Theorem to find the length of the hypotenuse.

$(\text{Hypotenuse})^2=(\text{leg 1})^2+(\text{leg 2})^2$

$\text{Hypotenuse}=\sqrt{4^2+5^2}=\sqrt{41}\:cm$

Report an Error

Example Question #4 : Apply The Pythagorean Theorem To Determine Unknown Side Lengths In Right Triangles: Ccss.Math.Content.8.G.B.7

Find the length of the hypotenuse in the right triangle below.

Possible Answers:

22.78

23.45

25.61

Correct answer:

25.61

Explanation:

Use the Pythagorean Theorem to find the hypotenuse.

$16^2+20^2=\text{Hypotenuse}^2$

$656=\text{Hypotenuse}^2$

$\sqrt{656}=25.61=\text{Hypotenuse}$

Report an Error

Example Question #1 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

If a right triangle has a base of and a height of , what is the length of the hypotenuse?

Possible Answers:

$\sqrt{14}$

$\sqrt{11}$

$\sqrt{65}$

Correct answer:

$\sqrt{65}$

Explanation:

To solve this problem, we must utilize the Pythagorean Theorom, which states that:

$a^{2}+b^{2}=c^{2}$

We know that the base is , so we can substitute in for . We also know that the height is , so we can substitute in for .

$7^{2}+4^{2}=c^{2}$

Next we evaluate the exponents:

$7^{2}=49$

$4^{2}=16$

Now we add them together:

49+16=65

Then, $65=c^{2}$ .

is not a perfect square, so we simply write the square root as $\sqrt{65}$ .

$c=\sqrt{65}$

Report an Error

Example Question #1 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

If a right triangle has a base of and a height of , what is the length of the hypotenuse?

Possible Answers:

$\sqrt{90}$

144

Correct answer:

$\sqrt{90}$

Explanation:

To solve this problem, we are going to use the Pythagorean Theorom, which states that $a^{2}+b^{2}=c^{2}$ .

We know that this particular right triangle has a base of , which can be substituted for , and a height of , which can be substituted for . If we rewrite the theorom using these numbers, we get:

$3^{2}+9^{2}=c^{2}$

Next, we evaluate the expoenents:

$3^{2}=9$

$9^{2}=81$

$9+81=c^{2}$

9+81=90

Then, $90=c^{2}$ .

To solve for , we must find the square root of . Since this is not a perfect square, our answer is simply $c=\sqrt{90}$ .

Report an Error

Example Question #2 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

What is the hypotenuse of a right triangle with sides 5 and 8?

Possible Answers:

100

$\sqrt{89}$

undefined

Correct answer:

$\sqrt{89}$

Explanation:

According to the Pythagorean Theorem, the equation for the hypotenuse of a right triangle is $a^{2} + b^{2}=c^{2}$ . Plugging in the sides, we get $5^{2}+8^{2}=c^{2}$ . Solving for , we find that the hypotenuse is $\sqrt{89}$ :

25+64=c^2

89=c^2

Report an Error

Example Question #3 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

In a right triangle, two sides have length . Give the length of the hypotenuse in terms of .

Possible Answers:

$\sqrt{3}t$

$2\sqrt{2}t$

$\sqrt{2}t$

$2\sqrt{3}t$

Correct answer:

$2\sqrt{2}t$

Explanation:

By the Pythagorean Theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Let hypotenuse and side length.

$c^2=s^2+s^2\Rightarrow c^2=(2t)^2+(2t)^2\Rightarrow c^2=8t^2\Rightarrow c=\sqrt{8t^2}=2\sqrt{2}t$

Report an Error

Example Question #2 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

In a right triangle, two sides have lengths 5 centimeters and 12 centimeters. Give the length of the hypotenuse.

Possible Answers:

$13\ cm$

$14.5\ cm$

$13.5\ cm$

$14\ cm$

$15\ cm$

Correct answer:

$13\ cm$

Explanation:

This triangle has two angles of 45 and 90 degrees, so the third angle must measure 45 degrees; this is therefore an isosceles right triangle.

By the Pythagorean Theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Let hypotenuse and , lengths of the other two sides.

$c^2=a^2+b^2\Rightarrow c^2=5^2+12^2\Rightarrow c^2=25+144=169$

$\Rightarrow c=\sqrt{169}\Rightarrow c=13\ cm$

Report an Error

Example Question #2 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

In a right triangle, the legs are 7 feet long and 12 feet long. How long is the hypotenuse?

Possible Answers:

193

$\sqrt{193}$

$3\sqrt{19$

Correct answer:

$\sqrt{193}$

Explanation:

The pythagorean theory should be used to solve this problem.

$a^{2}+b^{2}+=c^{2}$

$7^{2}+12^{2}+=c^{2}$

$49+144=c^{2}$

$193=c^{2}$

$\sqrt{193}=c$

Report an Error

View Tutors

David
Certified Tutor

Kent State University, Bachelors, Marketing. Kent State University at Kent, Masters in Education, Special Education.

View Tutors

Amanda
Certified Tutor

Seattle University, Current Undergrad Student, Applied Mathematics.

View Tutors

Sam
Certified Tutor

State University of New York at Albany, Bachelor in Arts, Mathematics.

All Common Core: 8th Grade Math Resources

7 Diagnostic Tests 75 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Calculus Tutors in Denver, Physics Tutors in Dallas Fort Worth, Calculus Tutors in Seattle, ACT Tutors in Miami, SSAT Tutors in Seattle, English Tutors in San Francisco-Bay Area, Biology Tutors in San Francisco-Bay Area, GMAT Tutors in San Francisco-Bay Area, Calculus Tutors in San Francisco-Bay Area, Statistics Tutors in Washington DC

Popular Courses & Classes

GRE Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Seattle, SAT Courses & Classes in Denver, GRE Courses & Classes in Chicago, ACT Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Atlanta, GRE Courses & Classes in Phoenix, SAT Courses & Classes in Washington DC, Spanish Courses & Classes in New York City, LSAT Courses & Classes in Boston

Popular Test Prep

MCAT Test Prep in New York City, LSAT Test Prep in Washington DC, SAT Test Prep in Philadelphia, GMAT Test Prep in Los Angeles, SAT Test Prep in Denver, GMAT Test Prep in Seattle, ISEE Test Prep in San Diego, SAT Test Prep in Chicago, LSAT Test Prep in New York City, GMAT Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Common Core: 8th Grade Math : Apply the Pythagorean Theorem to Determine Unknown Side Lengths in Right Triangles: CCSS.Math.Content.8.G.B.7

Study concepts, example questions & explanations for Common Core: 8th Grade Math

All Common Core: 8th Grade Math Resources

Example Questions

Example Question #1 : Apply The Pythagorean Theorem To Determine Unknown Side Lengths In Right Triangles: Ccss.Math.Content.8.G.B.7

Example Question #2 : Apply The Pythagorean Theorem To Determine Unknown Side Lengths In Right Triangles: Ccss.Math.Content.8.G.B.7

Example Question #3 : Apply The Pythagorean Theorem To Determine Unknown Side Lengths In Right Triangles: Ccss.Math.Content.8.G.B.7

Example Question #4 : Apply The Pythagorean Theorem To Determine Unknown Side Lengths In Right Triangles: Ccss.Math.Content.8.G.B.7

Example Question #1 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

Example Question #1 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

Example Question #2 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

Example Question #3 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

Example Question #2 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

Example Question #2 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

All Common Core: 8th Grade Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: