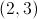We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Common Core: 8th Grade Math : Solve Systems of Two Linear Equations: CCSS.Math.Content.8.EE.C.8b

Study concepts, example questions & explanations for Common Core: 8th Grade Math

Create An Account

All Common Core: 8th Grade Math Resources

7 Diagnostic Tests 75 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Solution For A System Of Equations

3x + y = 8

2x + 4y = 12

Solve the system for and .

Possible Answers:

x = 2, y = 2

x = 10, y = -2

x = 3, y = -1

x = 2, y = 0

x = -4, y = 20

Correct answer:

x = 2, y = 2

Explanation:

The most simple method for solving systems of equations is to transform one of the equations so it allows for the canceling out of a variable. In this case, we can multiply 3x + y = 8 by (-4) to get -12x - 4y = -32 .

Then, we can add 2x + 4y = 12 to this equation to yield -10x = -20 , so x = 2 .

We can plug that value into either of the original equations; for example, 3(2) )+ y = 8 .

So, y = 2 as well.

Report an Error

Example Question #1 : Solve Systems Of Two Linear Equations: Ccss.Math.Content.8.Ee.C.8b

What is the solution to the following system of equations:

3x+5y = 15

3x+3y = 15

Possible Answers:

x=3,y=2

x = 5, y = 0

$x=3,y=\frac{6}{5}$

$x=2,y=\frac{13}{4}$

$x=\frac{1}{3},y=3$

Correct answer:

x = 5, y = 0

Explanation:

By solving one equation for , and replacing in the other equation with that expression, you generate an equation of only 1 variable which can be readily solved.

Report an Error

Example Question #3 : How To Find The Solution For A System Of Equations

Solve this system of equations for :

3x + 5y = 1

6x-y = 24

Possible Answers:

None of the other choices are correct.

$3\frac{1}{3}$

$2\frac{2}{3}$

$3\frac{2}{3}$

Correct answer:

$3\frac{2}{3}$

Explanation:

Multiply the bottom equation by 5, then add to the top equation:

6x-y = 24

$5 \left (6x-y \right ) =5\cdot 24$

30x-5y =120

$\underline{\textrm{\; } 3x + 5y = \; \; 1}$

$33x \;\;\;\;\;\; \; =121$

$x = \frac{121}{33} = \frac{11}{3} = 3 \frac{2}{3}$

Report an Error

Example Question #2 : Solve Systems Of Two Linear Equations: Ccss.Math.Content.8.Ee.C.8b

Solve this system of equations for :

3x + 5y = 23

6x-y = -9

Possible Answers:

y = 5

None of the other choices are correct.

$y = 3 \frac{1}{2}$

$y = 2 \frac{1}{2}$

y = 3

Correct answer:

y = 5

Explanation:

Multiply the top equation by :

3x + 5y = 23

$-2 \cdot \left (3x + 5y \right )= -2 \cdot 23$

$-6x -10y \right )= -46$

Now add:

$6x-\; \; y = -9$

$\underline{-6x -10y = -46}$

-11y = - 55

$-11y \div (-11) = -55\div (-11)$

y = 5

Report an Error

Example Question #3 : Solve Systems Of Two Linear Equations: Ccss.Math.Content.8.Ee.C.8b

Solve this system of equations for :

3x + 5y = 1

6x-y = 24

Possible Answers:

$y = -2 \frac{1}{5}$

y = -2

None of the other choices are correct.

$y = -1 \frac{3}{5}$

$y = -1 \frac{4}{5}$

Correct answer:

y = -2

Explanation:

Multiply the top equation by :

3x + 5y = 1

$-2 \cdot \left (3x + 5y \right )= -2 \cdot 1$

$-6x -10y \right )= -2$

Now add:

$\; \; 6x-\; \; \; y = 24$

$\underline{-6x -10y= -2} \right )$

-11y = 22

$-11y \div (-11) = 22\div (-11)$

y = -2

Report an Error

Example Question #151 : Systems Of Equations

Find the solution to the following system of equations.

a + 3b = 5

a-2b = 0

Possible Answers:

$a = 1,\ b = 2$

$a = 2,\ b = 1$

$a = 2,\ b = 2$

$a = 1,\ b = 1$

$a = 2,\ b = 3$

Correct answer:

$a = 2,\ b = 1$

Explanation:

a + 3b = 5

a-2b = 0

To solve this system of equations, use substitution. First, convert the second equation to isolate $\small a$ .

$a-2b = 0\rightarrow a=2b$

Then, substitute $\small 2b$ into the first equation for $\small a$ .

a + 3b = 5

(2b) + 3b = 5

Combine terms and solve for $\small b$ .

5b=5

b=1

Now that we know the value of $\small b$ , we can solve for $\small a$ using our previous substitution equation.

a=2b=2(1)=2

Report an Error

Example Question #5 : How To Find The Solution For A System Of Equations

Find a solution for the following system of equations:

$\left\{\begin{matrix} x-2y-1=3\\ -x+2y+2=5 \end{matrix}\right.$

Possible Answers:

$\left ( 8,2 \right )$

$\left ( 4,0 \right )$

no solution

infinitely many solutions

Correct answer:

no solution

Explanation:

When we add the two equations, the and variables cancel leaving us with:

1=8 which means there is no solution for this system.

Report an Error

Example Question #1 : Solve Systems Of Two Linear Equations: Ccss.Math.Content.8.Ee.C.8b

Solve the set of equations:

3x+2y=12

4x-3y=-1

Possible Answers:

$\left ( 1,1 \right )$

$\left ( -1,-1 \right )$

$\left ( 4,0 \right )$

$\left ( 2,3 \right )$

Correct answer:

$\left ( 2,3 \right )$

Explanation:

Solve the first equation for :

3x+2y=12

2y=12-3x

$y=6-\frac{3}{2}x$

Substitute into the second equation:

$4x-3(6-\frac{3}{2}x)=-1$

$4x-18+\frac{9}{2}x=-1$

Multiply the entire equation by 2 to eliminate the fraction:

8x-36+9x=-2

17x-36=-2

17x=34

x=2

Using the value of , solve for :

3(2)+2y=12

6+2y=12

2y=6

y=3

Therefore, the solution is $\left ( 2,3 \right )$

Report an Error

Example Question #2 : Solve Systems Of Two Linear Equations: Ccss.Math.Content.8.Ee.C.8b

Solve the following system of equations:

y = 2x-2

y = 3x+6

Possible Answers:

x=4,y=16

x=-4,y=-10

x=-4,y=-6

x=-8, y=-18

x=8,y=14

Correct answer:

x=-8, y=-18

Explanation:

Set the two equations equal to one another:

2x - 2 = 3x + 6

Solve for x:

x = -8

Plug this value of x into either equation to solve for y. We'll use the top equation, but either will work.

y = 2 * (-8) - 2

y = -18

Report an Error

Example Question #3 : Solve Systems Of Two Linear Equations: Ccss.Math.Content.8.Ee.C.8b

Solve this system of equations for :

3x + 5y = 23

6x-y = -9

Possible Answers:

$-\frac{1}{3}$

$\frac{1}{3}$

$\frac{2}{3}$

$-\frac{2}{3}$

None of the other choices are correct.

Correct answer:

$-\frac{2}{3}$

Explanation:

Multiply the bottom equation by , then add to the top equation:

6x-y = -9

$5 \left (6x-y \right ) =5\cdot (-9)$

30x-5y = -45

$\underline{\textrm{\; } 3x + 5y = \; \; 23}$

$33x \;\;\;\;\;\; \; =-22$

Divide both sides by

$\frac{33x}{33}=-\frac{22}{33}$

$\frac{22}{33}=-\frac{2}{3}$

Report an Error

View Tutors

Sarah
Certified Tutor

New York University, Bachelor of Fine Arts, Drama.

View Tutors

Rainier
Certified Tutor

Norfolk State University, Bachelors, Physics.

View Tutors

Jamie
Certified Tutor

East Central University, Bachelors, Special Education.

All Common Core: 8th Grade Math Resources

7 Diagnostic Tests 75 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Spanish Tutors in Phoenix, GMAT Tutors in Seattle, Calculus Tutors in Phoenix, Statistics Tutors in Seattle, Calculus Tutors in Los Angeles, Statistics Tutors in Denver, Physics Tutors in Washington DC, SSAT Tutors in Miami, Reading Tutors in New York City, ACT Tutors in Boston

Popular Courses & Classes

Spanish Courses & Classes in Houston, SSAT Courses & Classes in Houston, MCAT Courses & Classes in Boston, MCAT Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Boston, GRE Courses & Classes in Chicago, MCAT Courses & Classes in Washington DC, ISEE Courses & Classes in Chicago, Spanish Courses & Classes in San Diego, ISEE Courses & Classes in Atlanta

Popular Test Prep

ACT Test Prep in Atlanta, SAT Test Prep in Chicago, LSAT Test Prep in Phoenix, SAT Test Prep in San Francisco-Bay Area, ISEE Test Prep in Houston, SAT Test Prep in Atlanta, LSAT Test Prep in Miami, SAT Test Prep in Phoenix, GMAT Test Prep in Los Angeles, LSAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Common Core: 8th Grade Math : Solve Systems of Two Linear Equations: CCSS.Math.Content.8.EE.C.8b

Study concepts, example questions & explanations for Common Core: 8th Grade Math

All Common Core: 8th Grade Math Resources

Example Questions

Example Question #1 : How To Find The Solution For A System Of Equations

Example Question #1 : Solve Systems Of Two Linear Equations: Ccss.Math.Content.8.Ee.C.8b

Example Question #3 : How To Find The Solution For A System Of Equations

Example Question #2 : Solve Systems Of Two Linear Equations: Ccss.Math.Content.8.Ee.C.8b

Example Question #3 : Solve Systems Of Two Linear Equations: Ccss.Math.Content.8.Ee.C.8b

Example Question #151 : Systems Of Equations

Example Question #5 : How To Find The Solution For A System Of Equations

Example Question #1 : Solve Systems Of Two Linear Equations: Ccss.Math.Content.8.Ee.C.8b

Example Question #2 : Solve Systems Of Two Linear Equations: Ccss.Math.Content.8.Ee.C.8b

Example Question #3 : Solve Systems Of Two Linear Equations: Ccss.Math.Content.8.Ee.C.8b

All Common Core: 8th Grade Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: