All Differential Equations Resources
Example Questions
Example Question #1 : Transforms Of Periodic Functions
Find the Laplace transform of the periodic function.
Possible Answers:
Correct answer:
Explanation:
This particular piecewise function is called a square wave. The period of this function is the length at which it takes the function to return to its starting point.
For this particular function
it has a period of

and furthermore,
Using the Transform of a Periodic Function Theorem which states,
the problem can be solved as follows.
Shivansh
Certified Tutor
Certified Tutor
University of British Columbia, Bachelor, Math major and data science minor .
All Differential Equations Resources
Popular Subjects
Spanish Tutors in San Diego, ISEE Tutors in Chicago, GMAT Tutors in Philadelphia, Algebra Tutors in Philadelphia, Biology Tutors in Washington DC, ACT Tutors in New York City, GMAT Tutors in Miami, Physics Tutors in New York City, Calculus Tutors in Dallas Fort Worth, ACT Tutors in Seattle
Popular Courses & Classes
SSAT Courses & Classes in Miami, ISEE Courses & Classes in Houston, SAT Courses & Classes in Denver, GMAT Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Philadelphia, GMAT Courses & Classes in New York City, GMAT Courses & Classes in Miami, ACT Courses & Classes in Chicago, SSAT Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in Phoenix
Popular Test Prep
ACT Test Prep in Chicago, ISEE Test Prep in San Francisco-Bay Area, GRE Test Prep in Houston, ISEE Test Prep in Houston, SAT Test Prep in Denver, SSAT Test Prep in Atlanta, GRE Test Prep in Miami, MCAT Test Prep in Phoenix, GRE Test Prep in Denver, SSAT Test Prep in San Francisco-Bay Area







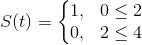

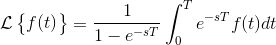

![\\=\frac{1}{1-e^{-4s}}\left[ \int_0^2 e^{-st}\cdot 1 dt+\int_2^4 e^{-st}\cdot 0dt \right] \\\\=\frac{1}{1-e^{-4s}}\frac{1-e^{-s}}{s}\\\\\leftarrow 1-e^{-4s}=(1+e^{-2s})(1-e^{-2s})\\\\\leftarrow (1-e^{-2s})=(1+e^{-s})(1-e^{-s}) \\\\=\frac{1-e^{-s}}{s(1+e^{-2s})(1-e^{-s})(1+e^{-s})} \\\\=\frac{1}{s(1+e^{-2s})(1+e^{-s})}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1003598/gif.latex)


