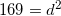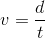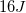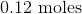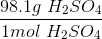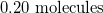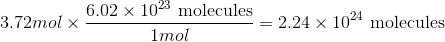Newton's Second Law is best represented as an equation, in which the product of mass and acceleration is equal to net force:

\(\displaystyle F_{net}=ma\)

By this principle, if there is zero acceleration, then the force must also be zero.

\(\displaystyle F_{net}=m(0\frac{m}{s^2})=0N\)

A non-zero acceleration must be present if there is a non-zero net force.

Newton's Third Law states that for every action there is an equal and opposite reaction. In other words, a force will act in equal and opposite directions on the two objects involved.

Weight and normal force are a specific example of this principle. Acceleration due to gravity creates a downward force, known as weight. This force, however, results in zero downward acceleration when the object is resting on a surface (a book does not fall through a table, for example). For the forces to be in equilibrium, there must be a counteracting upward force. This is known as the normal force, which is equal and opposite to the weight of the object. While weight pulls the object down, normal force pushes it up to create equilibrium.

The car has covered a total distance of \(\displaystyle \small 17\) miles, however, displacement and distance are not the same thing. Distance is simply the measure of how far the car have moved, regardless of direction. Displacement is a vector quantity, and takes direction into account. Displacement measures the total distance only between the car's starting point and ending point.

To solve this question, it is best to draw a sketch. The resulting sketch will be a right triangle with the hypotenuse equal to the displacement. The Pythagorean Theorem can be used to solve the problem.

\(\displaystyle \small a^2+b^2=c^2\)

\(\displaystyle \small 5^2+12^2=d^2\)

\(\displaystyle \small 25+144=d^2\)

\(\displaystyle \small 169=d^2\)

\(\displaystyle \small \sqrt{169}=\sqrt{d^2}\)

\(\displaystyle \small 13=d\)

This question requires us to convert between units, then solve for the velocity.

First, convert kilometers to meters. There are 1000m in 1km.

\(\displaystyle 144km\times \frac{1000m}{1km}=144000m\)

Then, convert hours to seconds. There are 60min in 1hr, and 60sec in 1min. In other words, there are 3600s in 1hr.

\(\displaystyle 2hr\times \frac{60min}{1hr}\times \frac{60s}{1hr}=7200s\)

Now that you have both the distance in meters and the time in seconds, you can find the velocity. Velocity is equal to the distance divided by the time.

\(\displaystyle v=\frac{d}{t}\)

\(\displaystyle v=\frac{144000m}{7200s}=20\frac{m}{s}\)

Kinetic energy (measured in Joules) can be solved using the equation:

\(\displaystyle KE=\frac{1}{2}mv^2\)

We are given both the mass of the projectile (2kg) and its velocity (\(\displaystyle \small 4\frac{m}{s}\)). Using these values, we can solve the equation.
\(\displaystyle KE=\frac{1}{2}(2kg)(4\frac{m}{s})^2\)

\(\displaystyle KE=\frac{1}{2}(2kg)(16\frac{m^2}{s^2})\)

\(\displaystyle KE=16\frac{kg\cdot m^2}{s^2}=16J\)

The amplitude measures the greatest displacement (either positive or negative) of a wave from the x-axis. Visually, the amplitude appears to be the distance from the x-axis (center line) to the top of one peak. In the figure, this value is given by A.

The other relevant measure given in the figure is segment D, which measures the distance between two peaks. This distance is known as the wavelength.

Segments B and C do not provide useful measurements of the wave function.

The movement of particles is important in differentiating the states of matter. Solids have the lowest molecular energy; their molecules barely vibrate and are generally trapped in lattice structures. Molecules in liquids are able to move more freely, resulting in the fluidity of the liquid state. Gas molecules have even more freedom of movement, allowing the gas to expand to fill a space.

Consider that energy (such as heat) must be added to convert a solid to a liquid or a liquid to a gas. That energy goes to make the molecules move faster and increase the temperature of the compound. Gases require the most energy (consider boiling water), and will have the fastest moving molecules.

To convert grams to moles, use the molecular weight of the molecule. This is found by adding the mass of each atom.

\(\displaystyle H_2SO_4\rightarrow 2(H)+1(S)+4(O)\)

\(\displaystyle 2(1.0\frac{g}{mol})+(32.1\frac{g}{mol})+4(16.0\frac{g}{mol})=98.1\frac{g}{mol}\)

\(\displaystyle \frac{98.1g\ H_2SO_4}{1mol\ H_2SO_4}\)

Now we can use the molecular mass to convert the given mass in the question to moles. Make sure to align the values so that the units cancel out.

\(\displaystyle 12.05g\ H_2SO_4\times \frac{1mol\ H_2SO_4}{98.1g\ H_2SO_4}=0.12mol\ H_2SO_4\)

Convert from moles to molecules using Avogadro's number:

\(\displaystyle (\text{moles})\times(\frac{6.02\times10^{23}\text{molecules}}{\text{mole}})=\text{molecules}\)

Use the moles given in the question to solve.

\(\displaystyle 3.72mol\times \frac{6.02\times10^{23}\ \text{molecules}}{1mol}=2.24\times10^{24}\ \text{molecules}\)

There are two primary bond types: ionic bonds and covalent bonds. Ionic bonds involve the transfer of an electron between atoms, while covalent bonds require atoms to share an electron between them. Ionic bonds are the stronger of the two. Ionic bonds usually form between a metal and a non-metal (for example, NaCl), while covalent bonds usually form between two non-metals (for example, HCl).

Hydrogen bonds are a type of intermolecular force and are similar to a very weak covalent bond. Hydrogen bonds are not actual bonds, and do not chemically link atoms together; they are strictly physical interactions. Disulfide bonds are covalent bonds between sulfur atoms that help form protein structure.