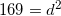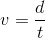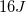Newton's Second Law is best represented as an equation, in which the product of mass and acceleration is equal to net force:

By this principle, if there is zero acceleration, then the force must also be zero.

A non-zero acceleration must be present if there is a non-zero net force.

Newton's Third Law states that for every action there is an equal and opposite reaction. In other words, a force will act in equal and opposite directions on the two objects involved.

Weight and normal force are a specific example of this principle. Acceleration due to gravity creates a downward force, known as weight. This force, however, results in zero downward acceleration when the object is resting on a surface (a book does not fall through a table, for example). For the forces to be in equilibrium, there must be a counteracting upward force. This is known as the normal force, which is equal and opposite to the weight of the object. While weight pulls the object down, normal force pushes it up to create equilibrium.

The car has covered a total distance of miles, however, displacement and distance are not the same thing. Distance is simply the measure of how far the car have moved, regardless of direction. Displacement is a vector quantity, and takes direction into account. Displacement measures the total distance only between the car's starting point and ending point.

To solve this question, it is best to draw a sketch. The resulting sketch will be a right triangle with the hypotenuse equal to the displacement. The Pythagorean Theorem can be used to solve the problem.

This question requires us to convert between units, then solve for the velocity.

First, convert kilometers to meters. There are 1000m in 1km.

Then, convert hours to seconds. There are 60min in 1hr, and 60sec in 1min. In other words, there are 3600s in 1hr.

Now that you have both the distance in meters and the time in seconds, you can find the velocity. Velocity is equal to the distance divided by the time.

Kinetic energy (measured in Joules) can be solved using the equation:

We are given both the mass of the projectile (2kg) and its velocity (). Using these values, we can solve the equation.

The amplitude measures the greatest displacement (either positive or negative) of a wave from the x-axis. Visually, the amplitude appears to be the distance from the x-axis (center line) to the top of one peak. In the figure, this value is given by A.

The other relevant measure given in the figure is segment D, which measures the distance between two peaks. This distance is known as the wavelength.

Segments B and C do not provide useful measurements of the wave function.