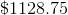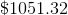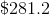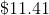Each year, you can calculate your interest by multiplying the principle () by . For one year, this would be:

For two years, it would be:

, which is the same as 

Therefore, you can solve for a five year period by doing:

Using your calculator, you can expand the  into a series of multiplications. This gives you , which is closest to . 

First, break the problem into two segments: the amount Jack invests in the high-yield savings, and the amount Jack invests in the simple interest account (10,000 and 5,000 respectively).

Now let's work with the high-yield savings account. $10,000 is invested at an annual rate of 8%, compounded quarterly. We can use the compound interest formula to solve:

Plug in the values given:

Therefore, Jack makes $824.32 off his high-yield savings account. Now let's calculate the other interest:

Add the two together, and we see that Jack makes a total of,  off of his investments.

It is easiest to break this down into steps. For each year, you will multiply by  to calculate the new value. Therefore, let's make a chart:

After year 1: ; Total interest: 

After year 2: ; Let us round this to ; Total interest: 

After year 3: ; Let us round this to ; Total interest: 

Thus, the positive difference of the interest from the last period and the interest from the first period is: 

Let's pick numbers. For quantitative comparisons with exponents, it's good to try 0, a negative number, and a fraction.

0: 0² = 0, 0³ = 0, so the two quantities are equal.

–1: (–1)² = 1, (–1)³ = –1, so Quantity A is greater.

Already we have a contradiction so the answer cannot be determined.

We know that the expression must be negative. Therefore one or all of the terms x⁷, y⁸ and z¹⁰ must be negative; however, even powers always produce positive numbers, so y⁸ and z¹⁰ will both be positive. Odd powers can produce both negative and positive numbers, depending on whether the base term is negative or positive. In this case, x⁷ must be negative, so x must be negative. Thus, the answer is x < 0.

First rewrite quantity B so that it has the same base as quantity A.

 can be rewriten as , which is equivalent to .  

Now we can compare the two quantities.

 is greater than .  

With problems like this, it is always best to break apart your values into their prime factors. Let's look at the numerator and the denominator separately:

Numerator

Continuing the simplification:

Now, these factors have in common a . Factor this out:

Denominator

This is much simpler:

Now, return to your fraction:

Cancel out the common factors of :

This problem is quite simple if you recall that the units place of powers of 2 follows a simple 4-step sequence. 

Observe the first few powers of 2:

2¹ = 2, 2² = 4, 2³ = 8, 2⁴ = 16, 2⁵ = 32, 2⁶ = 64, 2⁷ = 128, 2⁸ = 256 . . .

The units place follows a sequence of 2, 4, 8, 6, 2, 4, 8, 6, etc. Thus, divide 102 by 4. This gives a remainder of 2.  

The second number in the sequence is 4, so the answer is 4.

For exponent problems like this, the easiest thing to do is to break down all the numbers that you have into their prime factors. Begin with the number given to you:

Now, in order for you to have a number that is a multiple of this, you will need to have at least  in the prime factorization of the given number.  For each of the answer choices, you have:

; This is the answer.

Because the numbers involved in your fraction are so large, you are going to need to do some careful manipulating to get your answer. (A basic calculator will not work for something like this.) These sorts of questions almost always work well when you isolate the large factors and notice patterns involved. Let's first focus on the numerator. Go ahead and break apart the  into its prime factors:

Note that these have a common factor of . Therefore, you can rewrite the numerator as:

Now, put this back into your fraction: