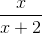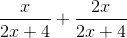GRE Math : How to add rational expressions with different denominators

Study concepts, example questions & explanations for GRE Math

Create An Account

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Rational Expressions

Simplify the expression.

$\frac{x}{2x+4}+\frac{x}{x+2}$

Possible Answers:

$\frac{x}{x+2}$

$\frac{1}{2x+4}$

$\frac{x+1}{2x+4}$

$\frac{2x}{3x+6}$

$\frac{3x}{2x+4}$

Correct answer:

$\frac{3x}{2x+4}$

Explanation:

To add rational expressions, first find the least common denominator. Because the denominator of the first fraction factors to 2(x+2), it is clear that this is the common denominator. Therefore, multiply the numerator and denominator of the second fraction by 2.

$\frac{x}{2x+4}+\frac{x}{x+2}$

$\frac{x}{2x+4}+\frac{(2)x}{(2)(x+2)}$

$\frac{x}{2x+4}+\frac{2x}{2x+4}$

$\frac{3x}{2x+4}$

This is the most simplified version of the rational expression.

Report an Error

Example Question #1 : Expressions

Simplify the following:

$\frac{x+3}{x-2}+\frac{x-2}{x+3}$

Possible Answers:

2x^2-4x+4

$\frac{2(x+3)(x-2)}{(x+3)(x-2)}$

$\frac{(x+3)^2+(x-2)^2}{(x+3)(x-2)}$

Correct answer:

$\frac{(x+3)^2+(x-2)^2}{(x+3)(x-2)}$

Explanation:

To simplify the following, a common denominator must be achieved. In this case, the first term must be multiplied by (x+2) in both the numerator and denominator and likewise with the second term with (x-3).

$\frac{(x+3)(x+3)}{(x-2)(x+3)}+\frac{(x-2)(x-2)}{(x+3)(x-2)}$

$\frac{(x+3)^2+(x-2)^2}{(x+3)(x-2)}$

Report an Error

Example Question #1 : How To Add Rational Expressions With Different Denominators

Choose the answer which best simplifies the following expression:

$\frac{3a^2 + a}{2} + \frac{10}{2a^2-a}$

Possible Answers:

$\frac{6a^4 - a^3 - a^2 + 20}{4a^2 + 2a}$

$\frac{6a^4 - a^3 - a^2 + 20}{4a^2 - 2a}$

$\frac{6a^4 + a^3 + a^2 + 20}{4a^2 - 2a}$

$\frac{36a^4 - a^3 - a^2 + 20}{4a^2 - 2a}$

$\frac{5a^3 - a^2 + 20}{4a^2 - 2a}$

Correct answer:

$\frac{6a^4 - a^3 - a^2 + 20}{4a^2 - 2a}$

Explanation:

To simplify, first multiply both terms by the denominator of the other term over itself:

$\frac{3a^2 + a}{2} \left(\frac{2a^2 - a}{2a^2 - a}\right) + \frac{10}{2a^2-a}\left(\frac{2}{2}\right)$

$\frac{6a^4 + 2a^3 -3a^3 - a^2}{4a^2 -2a} + \frac{20}{4a^2 - 2a}$

Then, you can combine the terms, now that they share a denominator:

$\frac{6a^4 - a^3 -a^2 +20}{4a^2 - 2a}$

Report an Error

Example Question #1 : How To Add Rational Expressions With Different Denominators

Choose the answer which best simplifies the following expression:

$\frac{3p}{2} + \frac{2p}{p^3}$

Possible Answers:

$\frac{3p^3 +4}{2p^2}$

$\frac{6p^4+8p}{4p^3}$

$\frac{3p^3+4p}{2p^3}$

$\frac{3p^4+2p}{2p^3}$

$\frac{3p^4+4p}{p^3}$

Correct answer:

$\frac{3p^3 +4}{2p^2}$

Explanation:

To simplify this expression, you have to get both numerators over a common denominator. The best way to go about doing so is to multiply both expressions by the others denominator over itself:

$\frac{3p}{2} \cdot \frac{p^3}{p^3 } + \frac{2p}{p^3} \cdot \frac{2}{2}$

Then you are left with:

$\frac{3p^4}{2p^3} + \frac{4p}{2p^3}$

Which you can simplify into:

$\frac{3p^4+4p}{2p^3}$

From there, you can take out a :

$\frac{p(3p^3 + 4)}{p(2p^2)}$

Which gives you your final answer:

$\frac{3p^3 +4}{2p^2}$

Report an Error

Example Question #3 : How To Add Rational Expressions With Different Denominators

Choose the answer which best simplifies the following expression:

$\frac{2a + 2}{3} + \frac{3}{a^2}$

Possible Answers:

$\frac{2a^3 + 2a^2 + 9}{3a}$

$\frac{2a^3 + 2a^2 + 3}{3a^2}$

$\frac{2a^3 + 2a^2 + 9}{3a^2}$

$\frac{2a^3 + 2a^2 + 9}{3a^3}$

$\frac{2a^2 + 2a + 9}{3a^2}$

Correct answer:

$\frac{2a^3 + 2a^2 + 9}{3a^2}$

Explanation:

To solve this problem, first multiply both terms of the expression by the denominator of the other over itself:

$\frac{2a + 2}{3} \cdot \frac{a^2}{a^2} + \frac{3}{a^2} \cdot \frac{3}{3}$

$\frac{2a^3 +2a^2}{3a^2} + \frac{9}{3a^2}$

Now that both terms have a common denominator, you can add them together:

$\frac{2a^3 +2a^2 + 9}{3a^2}$

Report an Error

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ACT Tutors in Washington DC, Math Tutors in San Francisco-Bay Area, Statistics Tutors in Phoenix, Physics Tutors in San Francisco-Bay Area, LSAT Tutors in Chicago, MCAT Tutors in San Diego, LSAT Tutors in San Francisco-Bay Area, SSAT Tutors in Atlanta, Biology Tutors in Houston, ACT Tutors in Chicago

Popular Courses & Classes

LSAT Courses & Classes in Atlanta, SSAT Courses & Classes in Atlanta, LSAT Courses & Classes in Boston, GMAT Courses & Classes in Philadelphia, MCAT Courses & Classes in Denver, MCAT Courses & Classes in San Diego, SAT Courses & Classes in Washington DC, SAT Courses & Classes in Denver, GRE Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Miami

Popular Test Prep

SSAT Test Prep in Chicago, SAT Test Prep in Chicago, ACT Test Prep in Philadelphia, SSAT Test Prep in Los Angeles, LSAT Test Prep in Atlanta, ISEE Test Prep in Chicago, GRE Test Prep in Phoenix, ACT Test Prep in Dallas Fort Worth, MCAT Test Prep in San Francisco-Bay Area, ISEE Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

Email address:
Your name:
Feedback:

GRE Math : How to add rational expressions with different denominators

Study concepts, example questions & explanations for GRE Math

All GRE Math Resources

Example Questions

Example Question #1 : Rational Expressions

Example Question #1 : Expressions

Example Question #1 : How To Add Rational Expressions With Different Denominators

Example Question #1 : How To Add Rational Expressions With Different Denominators

Example Question #3 : How To Add Rational Expressions With Different Denominators

All GRE Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details