GRE Math : How to find a rational number from an exponent

Study concepts, example questions & explanations for GRE Math

Create An Account

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find A Rational Number From An Exponent

Quantitative Comparison: Compare Quantity A and Quantity B, using additional information centered above the two quantities if such information is given.

Quantity A Quantity B

4³3⁴

Possible Answers:

The two quantities are equal.

The answer cannot be determined from the information given.

Quantity A is greater.

Quantity B is greater.

Correct answer:

Quantity B is greater.

Explanation:

In order to determine the relationship between the quantities, solve each quantity.

4³is 4 * 4 * 4 = 64

3⁴ is 3 * 3 * 3 * 3 = 81

Therefore, Quantity B is greater.

Report an Error

Example Question #2 : How To Find A Rational Number From An Exponent

Quantity A: $(-1)^{137}$ $\displaystyle (-1)^{137}$

Quantity B: $\displaystyle 0$

Possible Answers:

The relationship cannot be determined from the information given.

Quantity A is greater.

Quantity B is greater.

The two quantities are equal.

Correct answer:

Quantity B is greater.

Explanation:

(–1) ¹³⁷= –1

–1 < 0

(–1) ^{odd #} always equals –1.

(–1) ^{even #} always equals +1.

Report an Error

Example Question #33 : Algebra

$2^{-5}$ $\displaystyle 2^{-5}$

Possible Answers:

$\displaystyle 2$

$\frac{1}{32}$ $\displaystyle \frac{1}{32}$

$\displaystyle 32$

$\displaystyle -32$

$-\frac{1}{32}$ $\displaystyle -\frac{1}{32}$

Correct answer:

$\frac{1}{32}$ $\displaystyle \frac{1}{32}$

Explanation:

Anything raised to negative power means $\displaystyle 1$ over the base raised to the postive exponent.

$2^{-5}=\frac{1}{2^5}=\frac{1}{32}$ $\displaystyle 2^{-5}=\frac{1}{2^5}=\frac{1}{32}$

Report an Error

Example Question #15 : Exponents And Rational Numbers

Which of the following is not the same as the others?

Possible Answers:

16^8 $\displaystyle 16^8$

$2^{24}$ $\displaystyle 2^{24}$

$(\frac{1}{2})^{^{-24}}$ $\displaystyle (\frac{1}{2})^{^{-24}}$

64^4 $\displaystyle 64^4$

$4^{12}$ $\displaystyle 4^{12}$

Correct answer:

16^8 $\displaystyle 16^8$

Explanation:

Let's all convert the bases to $\displaystyle 2$.

$4^{12}=[2^2]^{12}=2^{24}$ $\displaystyle 4^{12}=[2^2]^{12}=2^{24}$

$64^4=(2^6)^4=2^{24}$ $\displaystyle 64^4=(2^6)^4=2^{24}$

$16^8=[2^4]^8=2^{32}$ $\displaystyle 16^8=[2^4]^8=2^{32}$

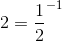
$\left(\frac{1}{2}\right)^{^{-24}}$ $\displaystyle \left(\frac{1}{2}\right)^{^{-24}}$ This one may be intimidating but $2=\frac{1}{2}^{-1}$ $\displaystyle 2=\frac{1}{2}^{-1}$.

Therefore,

$\left(\left[\frac{1}{2}\right]^{-24}\right)^{-1}=2^{24}$ $\displaystyle \left(\left[\frac{1}{2}\right]^{-24}\right)^{-1}=2^{24}$

$2^{24}$ $\displaystyle 2^{24}$

16^8 $\displaystyle 16^8$ is not like the answers so this is the correct answer.

Report an Error

Example Question #41 : Exponents

Simplify

$2^{10}+2^9$ $\displaystyle 2^{10}+2^9$

Possible Answers:

$2^{18}\cdot 3$ $\displaystyle 2^{18}\cdot 3$

$2^9\cdot 3$ $\displaystyle 2^9\cdot 3$

$2^{10}$ $\displaystyle 2^{10}$

$2^{19}$ $\displaystyle 2^{19}$

$2^{10}\cdot 3$ $\displaystyle 2^{10}\cdot 3$

Correct answer:

$2^9\cdot 3$ $\displaystyle 2^9\cdot 3$

Explanation:

Whenever you see lots of multiplication (e.g. exponents, which are notation for repetitive multiplication) separated by addition or subtraction, a common way to transform the expression is to factor out common terms on either side of the + or - sign. That allows you to create more multiplication, which is helpful in reducing fractions or in reducing the addition/subtraction to numbers you can quickly calculate by hand as you'll see here.

So let's factor a 2^9 $\displaystyle 2^9$.

We have $\displaystyle 2^9(2+1)$.

And you'll see that the addition inside parentheses becomes quite manageable, leading to the final answer of $2^9\cdot 3$ $\displaystyle 2^9\cdot 3$.

Report an Error

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ACT Tutors in Phoenix, Algebra Tutors in Seattle, Algebra Tutors in San Francisco-Bay Area, Biology Tutors in Denver, LSAT Tutors in New York City, Reading Tutors in Denver, Algebra Tutors in Houston, French Tutors in Houston, MCAT Tutors in Dallas Fort Worth, Chemistry Tutors in Phoenix

Popular Courses & Classes

SSAT Courses & Classes in San Diego, GMAT Courses & Classes in Miami, LSAT Courses & Classes in Los Angeles, MCAT Courses & Classes in Denver, SSAT Courses & Classes in Denver, ACT Courses & Classes in Philadelphia, MCAT Courses & Classes in Seattle, ACT Courses & Classes in Houston, GMAT Courses & Classes in Seattle, SSAT Courses & Classes in Seattle

Popular Test Prep

SSAT Test Prep in Atlanta, LSAT Test Prep in Dallas Fort Worth, SSAT Test Prep in Los Angeles, MCAT Test Prep in Seattle, GMAT Test Prep in Seattle, SSAT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Seattle, ISEE Test Prep in Washington DC, SSAT Test Prep in Miami, ACT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

Email address:
Your name:
Feedback:

GRE Math : How to find a rational number from an exponent

Study concepts, example questions & explanations for GRE Math

All GRE Math Resources

Example Questions

Example Question #1 : How To Find A Rational Number From An Exponent

Example Question #2 : How To Find A Rational Number From An Exponent

Example Question #33 : Algebra

Example Question #15 : Exponents And Rational Numbers

Example Question #41 : Exponents

All GRE Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details