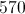Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Data Properties

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Range For A Set Of Data

Six homes are for sale and have the following dollar values in thousands of dollars:

535

155

305

720

315

214

What is the range of the values of the six homes?

Possible Answers:

565

346

374

535

155

Correct answer:

565

Explanation:

The range is the simplest measurement of the difference between values in a data set. To find the range, one simply subtracts the lowest value from the greatest value, ignoring the others. Here, the lowest value is 155 and the greatest is 720.

720 - 155 = 565

Report an Error

Example Question #1 : How To Find The Range For A Set Of Data

Alice recorded the outside temperature at noon each day for one week. These were the results.

Monday: 78

Tuesday: 85

Wednesday: 82

Thursday: 84

Friday: 82

Saturday: 79

Sunday: 80

What is the range of temperatures?

Possible Answers:

81.4

83.7

570

Correct answer:

Explanation:

The range is the simplest measurement of the difference between values in a data set. To find the range, simply subtract the lowest value from the greatest value, ignoring the others.

85-78=7

Report an Error

Example Question #1 : Data Properties

You are given the following data:

3, 7, 2, 3, 9, 12, 2, 3, 9, 0, 1

What is the range?

Possible Answers:

5.5

Correct answer:

Explanation:

Recall that we find the range of a set of data by subtracting the smallest value from the largest value. In this case, the smallest value is and the largest value is . Thus, our range is 12 - 0 = 12 .

Report an Error

Example Question #13 : Basic Statistics

There are girls and boys running a race. What is the probability that only boys will finish in the top three places?

Possible Answers:

$\frac{11}{15}$

$\frac{1}{6}$

$\frac{9}{20}$

$\frac{1}{30}$

$\frac{2}{5}$

Correct answer:

$\frac{1}{30}$

Explanation:

Probability is a fraction between and . The numerator is the total number of ways to get what you want, or a subset of the sample space. The denominator is the total ways, or complete sample space.

The number of ways only boys would finsih in the top three places: $4\cdot 3\cdot 2= 24$

The number of ways all contestants can finish the race: $10\cdot 9\cdot 8=720$

So the probability of only boys finishing in the top three places is given by the fraction $\frac{24}{720}= \frac{1}{30}$ when simplified.

Report an Error

Example Question #13 : Basic Statistics

is the ____________ of the following dataset below.

$\{20, 12, 17, 14, 12\}$

Possible Answers:

median

range

mean

mode

Correct answer:

median

Explanation:

Reorder the numerals in the set, from least to greatest.

$\{12, 12, 14, 17, 20\}$

The number in the middle is the median. $\{12, 12, \mathbf{14}, 17, 20\}$

The most frequent numeral is the mode. $\{\mathbf{12}, \mathbf{12}, 14, 17, 20\}$

The mean is the sum of the numerals divided by the number of data points.

$\frac{12+12+14+17+20}{5}=15$

The mean is 15.

The range is the difference between the maximum and the minimum.

20-12=8

The range is 8.

Report an Error

Example Question #14 : Basic Statistics

For the following data set:

$2,\; 5,\; 9,\; 3,\; 7,\; 12,\; 15,\; \; 10,\; 9$

Which is the smallest?

Possible Answers:

Mean

Median

None of the answers

Range

Mode

Correct answer:

Mean

Explanation:

Put the data in order from smallest to largest and then calculate each stastic: mean, mode, median, range

$2,\;3,\;5,\;7,\;9,\;9,\;10,\;12,\;15$

Range = Max - Min or 15-2=13

Mode is the most often repeated number or

Median is the number in the middle or

Mean is the sum of the data divided by the number of data points or $\frac{\sum x}{n}= \frac{72}{9}=8$

Report an Error

Example Question #14 : Basic Statistics

1,1,2,3,6,8,10,11,12,15, 30

$\textup{What is the median of the above number set?}$

Possible Answers:

Correct answer:

Explanation:

$\textup{As the numbers are already listed in increasing order, the median is simply}$

$\textup{the one in the middle. In this case 8 is the 6th term counted from either side..}$

Report an Error

Example Question #1 : Understanding Mean, Median, And Mode

Find the median of the following number series:

3, 6, 27, 19, 8, 11, 30, 42, 7, 39

Possible Answers:

19.2

Correct answer:

Explanation:

The first step to finding the median is always to put the numbers in the proper order:

3, 6, 7, 8, 11, 19, 27, 30, 39, 42

When we have an even amount of numbers, we find the average (or mean) of the middle two to get the median:

11 + 19 = 30/2 = 15

Report an Error

Example Question #12 : Basic Statistics

With a standard deck of playing cards, what is the probability of picking one red card followed by one black card, without replacement?

Possible Answers:

$\frac{13}{51}$

$\frac{1}{26}$

$\frac{17}{52}$

$\frac{17}{25}$

$\frac{1}{4}$

Correct answer:

$\frac{13}{51}$

Explanation:

In a standard deck of playing cards we have:

$26\; red+26\; black=52\; cards$

So the probability of picking the first card red is $\frac{26}{52}=\frac{1}{2}$ .

Then the probability of picking the second card black is $\frac{26}{51}$ because this is without replacement.

They are independent events so the probabilities get multiplied together to give $\frac{13}{51}$ .

Report an Error

Example Question #5 : Understanding Mean, Median, And Mode

Which statement is true concerning the following data set:

2,5,9,3,4,7,3,8,11,15,10

Possible Answers:

range - mode = mean

mean=median

mode+mean = median

mode+median> range

mode> mean

mode+mean = median

Correct answer:

mean=median

Explanation:

First, put the data in order, smallest to largest:

2,3,3,4,5,7,8,9,10,11,15

$mean = \frac{\sum x}{n}=\frac{77}{11}=7$

mode=3

median = 7

range=max-min=15-2=13

Note, the mode is the number most often repeated in the data set and the median is the middle number.

So mean=median is the only true statement.

Report an Error

View Tutors

Satweka
Certified Tutor

The University of Texas at Dallas, Master of Science, Biomedical Engineering.

View Tutors

Jesse
Certified Tutor

University of Memphis, Master of Fine Arts, English.

View Tutors

Matthew
Certified Tutor

Bluffton University, Bachelor of Education, Mathematics. Bluffton University, Masters in Education, Education.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in Philadelphia, Statistics Tutors in Boston, Calculus Tutors in Seattle, SAT Tutors in San Francisco-Bay Area, LSAT Tutors in Houston, Biology Tutors in Dallas Fort Worth, LSAT Tutors in New York City, Math Tutors in Chicago, Algebra Tutors in Miami, GRE Tutors in Seattle

Popular Courses & Classes

GRE Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Philadelphia, GMAT Courses & Classes in Chicago, MCAT Courses & Classes in Seattle, SAT Courses & Classes in Denver, SSAT Courses & Classes in Los Angeles, ACT Courses & Classes in Miami, GMAT Courses & Classes in Miami, GMAT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in Los Angeles

Popular Test Prep

GMAT Test Prep in Boston, GRE Test Prep in Dallas Fort Worth, MCAT Test Prep in Houston, ISEE Test Prep in San Diego, GMAT Test Prep in Phoenix, ISEE Test Prep in San Francisco-Bay Area, GMAT Test Prep in Miami, MCAT Test Prep in Phoenix, ACT Test Prep in Miami, SAT Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Data Properties

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : How To Find The Range For A Set Of Data

Example Question #1 : How To Find The Range For A Set Of Data

Example Question #1 : Data Properties

Example Question #13 : Basic Statistics

Example Question #13 : Basic Statistics

Example Question #14 : Basic Statistics

Example Question #14 : Basic Statistics

Example Question #1 : Understanding Mean, Median, And Mode

Example Question #12 : Basic Statistics

Example Question #5 : Understanding Mean, Median, And Mode

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: