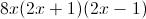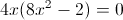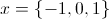We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Factoring Polynomials

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Factoring Polynomials

Factor $x^{3}-64$

Possible Answers:

(x-4)(x^2+4x+16)

(x-4)(x^2-4x-16)

(x+4)(x^2-4x+16)

Cannot be Factored

Correct answer:

(x-4)(x^2+4x+16)

Explanation:

Use the difference of perfect cubes equation:

a^3-b^3=(a-b)(a^2+ab+b^2)

In $x^{3}-64$ ,

a=x and $b=\sqrt[3]{64}=4$

(x-4)(x^2+(x)(4)+4^2)

(x-4)(x^2+4x+16)

Report an Error

Example Question #2 : Factoring Polynomials

Factor the polynomial completely and solve for .

Possible Answers:

8x(4x^2 -1)

$x = \left \{ -\frac{1}{2}, 0, \frac{1}{2} \right \}$

4x (8x^2 - 2) = 0

$x = \left \{0, \frac{1}{2} \right \}$

8x(2x+1)(2x-1)

$x = \left \{-\frac{1}{2}, 0, \frac{1}{2} \right \}$

32x(x+1)(x-1)

$x = \left \{ -1, 0,1\right \}$

8(4x^3- x)

x = 0

Correct answer:

8x(2x+1)(2x-1)

$x = \left \{-\frac{1}{2}, 0, \frac{1}{2} \right \}$

Explanation:

To factor and solve for in the equation

Factor out of the equation

$\rightarrow 8x(4x^2-1)$

Use the "difference of squares" technique to factor the parenthetical term, which provides the completely factored equation:

$\rightarrow 8x(2x+1)(2x-1)$

Any value that causes any one of the three terms , 2x+1 , and 2x -1 to be will be a solution to the equation, therefore

$x = \left \{-\frac{1}{2}, 0, \frac{1}{2} \right \}$

Report an Error

Example Question #1 : Factoring Polynomials

Factor the following expression:

x^2+xy+x=

Possible Answers:

x(x+y+1)

x(x+y)

x+y

x^2+x(y+1)

x+y+1

Correct answer:

x(x+y+1)

Explanation:

You can see that each term in the equation has an "x", therefore by factoring "x" from each term you can get that the equation equals x(x+y+1) .

Report an Error

Example Question #3 : Factoring Polynomials

Factor this expression:

x^2+7x+12

Possible Answers:

(x+4)(x+3)

(x+2) (x+6)

(x+4)(x-3)

(x-2) (x+6)

(x-4)(x+3)

Correct answer:

(x+4)(x+3)

Explanation:

First consider all the factors of 12:

1 and 12

2 and 6

3 and 4

Then consider which of these pairs adds up to 7. This pair is 3 and 4.

Therefore the answer is (x+4)(x+3) .

Report an Error

Example Question #41 : Intermediate Single Variable Algebra

Find the zeros.

$f(x)=x^{3}-1$

Possible Answers:

x=-1

x=10

x=1

x=1,-1

x=0

Correct answer:

x=1

Explanation:

This is a difference of perfect cubes so it factors to (x-1)(x^2+x+1) . Only the first expression will yield an answer when set equal to 0, which is 1. The second expression will never cross the -axis. Therefore, your answer is only 1.

Report an Error

Example Question #42 : Intermediate Single Variable Algebra

Find the zeros.

f(x)=2x^5-8x^3+8x

Possible Answers:

$x=0, \sqrt{2}, -\sqrt{2 }$

x=2,0

$x=\sqrt{2}$

x=0

$x= \sqrt{-2}}$

Correct answer:

$x=0, \sqrt{2}, -\sqrt{2 }$

Explanation:

Factor the equation to 2x(x^4-4x^2+4) . Set 2x=0 and get one of your 's to be . Then factor the second expression to (x^2-2) (x^2-2) . Set them equal to zero and you get $\pm \sqrt{2}$ .

Report an Error

Example Question #4 : Factoring Polynomials

Factor the following polynomial:

54a^3b-2b^4

Possible Answers:

2b(3a-b)(9a^2+2ab+b^2)

3b(3a-b)(9a^2+3ab+b^2)

2b(3a-b)(9a^2+3ab+b^2)

2b(2a-b)(9a^2+3ab+b^2)

3b(2a-b)(9a^2+3ab+b^2)

Correct answer:

2b(3a-b)(9a^2+3ab+b^2)

Explanation:

Begin by extracting from the polynomial:

54a^3b-2b^4

=2b(27a^3-b^3)

Now, factor the remainder of the polynomial as a difference of cubes:

=2b(3a-b)(9a^2+3ab+b^2)

Report an Error

Example Question #2 : Factoring Polynomials

Factor the following polynomial:

5ab+b^2+5ac-c^2

Possible Answers:

(b+c)(5a+b+c)

(b-c)(5a+b-c)

(b-c)(5a-b+c)

(b+c)(5a-b-c)

(b+c)(5a+b-c)

Correct answer:

(b+c)(5a+b-c)

Explanation:

Begin by rearranging like terms:

5ab+b^2+5ac-c^2

=5ab+5ac+b^2-c^2

Now, factor out like terms:

=5a(b+c)+(b+c)(b-c)

Rearrange the polynomial:

=(b+c)(5a+b-c)

Report an Error

Example Question #3 : Factoring Polynomials

Factor the following polynomial:

m^3-3m^2a+3ma^2-a^3

Possible Answers:

m-a

(m-a)^3

(m-a)^4

(m-a)^2

Correct answer:

(m-a)^3

Explanation:

Begin by rearranging like terms:

m^3-3m^2a+3ma^2-a^3

=m^3-a^3-3m^2a+3ma^2

Now, factor out like terms:

=(m-a)(m^2+ma+a^2)-3ma(m-a)

Rearrange the polynomial:

=(m-a)(m^2-2ma+a^2)

Factor:

=(m-a)(m-a)^2

=(m-a)^3

Report an Error

Example Question #2 : Factoring Polynomials

Factor the following polynomial:

12n^2-7n-10

Possible Answers:

(3n-5)(3n+3)

(4n-5)(3n+2)

(4n+5)(3n-2)

(4n-5)(4n+2)

(3n-5)(3n+2)

Correct answer:

(4n-5)(3n+2)

Explanation:

Begin by separating -7n into like terms. You do this by multiplying and , then finding factors which sum to

12n^2-7n-10

12n^2-15n+8n-10

Now, extract like terms:

3n(4n-5)+2(4n-5)

Simplify:

(4n-5)(3n+2)

Report an Error

View Tutors

Michael
Certified Tutor

Ferris State University, Bachelor of Science, Economics.

View Tutors

Ariel
Certified Tutor

Central Bicol State University of Agriculture, Doctor of Education, Child Development.

View Tutors

Angad
Certified Tutor

Guru Gobind Singh Indraprastha University, Bachelor of Technology, Mechanical Engineering. University of Northern British Col...

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

French Tutors in Los Angeles, SAT Tutors in Dallas Fort Worth, ISEE Tutors in Washington DC, SAT Tutors in Los Angeles, Spanish Tutors in New York City, English Tutors in New York City, Calculus Tutors in San Francisco-Bay Area, Statistics Tutors in Atlanta, English Tutors in Washington DC, Physics Tutors in Phoenix

Popular Courses & Classes

LSAT Courses & Classes in Phoenix, GRE Courses & Classes in Atlanta, LSAT Courses & Classes in Miami, ISEE Courses & Classes in Los Angeles, ACT Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Boston, SSAT Courses & Classes in Miami, Spanish Courses & Classes in Miami, GMAT Courses & Classes in Chicago, ISEE Courses & Classes in Chicago

Popular Test Prep

ACT Test Prep in San Francisco-Bay Area, ACT Test Prep in Philadelphia, SSAT Test Prep in San Francisco-Bay Area, GRE Test Prep in Atlanta, MCAT Test Prep in Atlanta, GMAT Test Prep in Chicago, MCAT Test Prep in Seattle, SAT Test Prep in Phoenix, ISEE Test Prep in New York City, ISEE Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Factoring Polynomials

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : Factoring Polynomials

Example Question #2 : Factoring Polynomials

Example Question #1 : Factoring Polynomials

Example Question #3 : Factoring Polynomials

Example Question #41 : Intermediate Single Variable Algebra

Example Question #42 : Intermediate Single Variable Algebra

Example Question #4 : Factoring Polynomials

Example Question #2 : Factoring Polynomials

Example Question #3 : Factoring Polynomials

Example Question #2 : Factoring Polynomials

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: