All High School Math Resources
Example Questions
Example Question #1 : Derivatives
Define 
Give the interval(s) on which 

<0)
We need to find the values of 
&space;=&space;3x%5E%7B2%7D&space;-18x+24&space;<0)
These are the boundary points, so the intervals we need to check are:


We check each interval by substituting an arbitrary value from each for 
Choose

Choose

Choose

The answer is that 

Example Question #2 : Derivatives
Define &space;=&space;x%5E%7B3%7D&space;-&space;%5Cfrac%7B21%7D%7B2%7D&space;x%5E%7B2%7D&space;+30x&space;-6)
Give the interval(s) on which 

>0)
We need to find the values of 

These are the boundary points, so the intervals we need to check are:


We check each interval by substituting an arbitrary value from each for 
Choose

Choose

Choose

The answer is that 
Example Question #1 : Derivatives
At what point does 
It does not shift from increasing to decreasing
To find out where the graph shifts from increasing to decreasing, we need to look at the first derivative.
To find the first derivative, we can use the power rule. We lower the exponent on all the variables by one and multiply by the original variable.
We're going to treat 

Notice that 
If we were to graph 
Example Question #1 : Finding Regions Of Increasing And Decreasing Value
At what point does 
To find out where it shifts from decreasing to increasing, we need to look at the first derivative. The shift will happen where the first derivative goes from a negative value to a positive value.
To find the first derivative for this problem, we can use the power rule. The power rule states that we lower the exponent of each of the variables by one and multiply by that original exponent.
Remember that anything to the zero power is one.
Can this equation be negative? Yes. Does it shift from negative to positive? Yes. Therefore, it will shift from negative to positive at the point that 
Example Question #681 : Derivatives
At what value of 

It does not shift from decreasing to increasing
To find out when the function shifts from decreasing to increasing, we look at the first derivative.
To find the first derivative, we can use the power rule. We lower the exponent on all the variables by one and multiply by the original variable.
Anything to the zero power is one.
From here, we want to know if there is a point at which graph changes from negative to positive. Plug in zero for y and solve for x.
This is the point where the graph shifts from decreasing to increasing.
All High School Math Resources




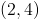
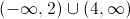

&space;=&space;3%5Ccdot&space;x%5E%7B3-1%7D&space;-2%5Ccdot&space;9x%5E%7B2-1%7D+24+0)















































































