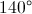We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : How to find an angle in a polygon

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find An Angle In A Polygon

What is the magnitude of the interior angle of a regular nonagon?

Possible Answers:

135^o

140^o

129^o

144^o

Correct answer:

140^o

Explanation:

The equation to calculate the magnitude of an interior angle is $\frac{180(n-2)}{n}=int\ angle$ , where is equal to the number of sides.

For our question, n=9 .

$int\ angle= \frac{180(9-2)}{9}=\frac{(180)(7)}{9}=140^o$

Report an Error

Example Question #12 : Other Polygons

What is the interior angle measure of any regular heptagon?

Possible Answers:

135

130.2

128.6

125.8

Correct answer:

128.6

Explanation:

To find the angle of any regular polygon you find the number of sides, . In this example, n=7 .

You then subtract 2 from the number of sides yielding 5.

Take 5 and multiply it by 180 degrees to yield the total number of degrees in the regular heptagon. 5*180=900

Then to find one individual angle we divide 900 by the total number of angles, 7.

$\frac{900}{7}=128.6$

The answer is 128.6 .

Report an Error

Example Question #13 : Other Polygons

A regular polygon with sides has exterior angles that measure $1.5^{\circ }$ each. How many sides does the polygon have?

Possible Answers:

120

180

This figure cannot exist.

240

150

Correct answer:

240

Explanation:

The sum of the exterior angles of any polygon, one per vertex, is $360 ^{\circ }$ . As each angle measures $1.5^{\circ }$ , just divide 360 by 1.5 to get the number of angles.

$360 \div 1.5=240$

Report an Error

Example Question #14 : Other Polygons

What is the interior angle measure of any regular nonagon?

Possible Answers:

$140^{\circ}$

$120^{\circ}$

$200^{\circ}$

$160^{\circ}$

Correct answer:

$140^{\circ}$

Explanation:

To find the angle of any regular polygon you find the number of sides , which in this example is .

You then subtract from the number of sides yielding .

Take and multiply it by 180 degrees to yield a total number of degrees in the regular nonagon.

7*180=1260

Then to find one individual angle we divide 1260 by the total number of angles .

$\frac{1260}{9}=140$

The answer is 140 .

Report an Error

Example Question #2 : How To Find An Angle In A Polygon

What is the measure of one exterior angle of a regular seventeen-sided polygon (nearest tenth of a degree)?

Possible Answers:

$25.2 ^{\circ }$

$15.9^{\circ }$

$34.0 ^{\circ }$

$21.2^{\circ }$

$10.6^{\circ }$

Correct answer:

$21.2^{\circ }$

Explanation:

The sum of the measures of the exterior angles of any polygon, one per vertex, is $360^{\circ}$ . In a regular polygon, all of these angles are congruent, so divide 360 by 17 to get the measure of one exterior angle:

$360 \div 17 \approx 21.2^{\circ }$

Report an Error

Example Question #2 : How To Find An Angle In A Polygon

What is the measure of one exterior angle of a regular twenty-three-sided polygon (nearest tenth of a degree)?

Possible Answers:

$15.7 ^{\circ }$

$7.8^{\circ }$

$14.4^{\circ }$

$28.8^{\circ }$

$31.3^{\circ }$

Correct answer:

$15.7 ^{\circ }$

Explanation:

The sum of the measures of the exterior angles of any polygon, one per vertex, is $360^{\circ}$ . In a regular polygon, all of these angles are congruent, so divide 360 by 23 to get the measure of one exterior angle:

$360 \div 23 \approx 15.7 ^{\circ }$

Report an Error

Example Question #21 : Geometry

What is the measure of one interior angle of a regular twenty-three-sided polygon (nearest tenth of a degree)?

Possible Answers:

$159.3^{\circ }$

$174.3^{\circ }$

$169.3^{\circ }$

$164.3^{\circ }$

$154.3^{\circ }$

Correct answer:

$164.3^{\circ }$

Explanation:

The measure of each interior angle of a regular polygon with sides is $\frac{180 (N-2)}{N}$ . We can substitute N = 23 to obtain the angle measure:

$\frac{180 (N-2)}{N} = \frac{180 (23-2)}{23} = \frac{180 \cdot 21}{23}\approx 164.3^{\circ }$

Report an Error

Example Question #5 : How To Find An Angle In A Polygon

A regular polygon has interior angles which measure $162^{\circ }$ each. How many sides does the polygon have?

Possible Answers:

Correct answer:

Explanation:

The easiest way to answer this is to note that, since an interior angle and an exterior angle form a linear pair - and thus, a supplementary pair - each exterior angle would have measure $180-162 = 18^{\circ }$ . Since 360 divided by the number of sides of a regular polygon is equal to the measure of one of its exterior angles, we are seeking such that

$\frac{360}{N} = 18$

Solve for :

$\frac{360}{N}\cdot N= 18\cdot N$

18N = 360

$18N \div 18= 360\div 18$

N = 20

The polygon has 20 sides.

Report an Error

View Tutors

Zachery
Certified Tutor

View Tutors

Novak
Certified Tutor

Algonquin College International Education Centre, Bachelor in Business Administration, Business Administration and Management.

View Tutors

Wendy
Certified Tutor

Marymount University, Master's/Graduate, Masters of Education.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

MCAT Tutors in Houston, SAT Tutors in New York City, ACT Tutors in San Diego, French Tutors in Boston, Chemistry Tutors in Philadelphia, SSAT Tutors in Dallas Fort Worth, Reading Tutors in Washington DC, Computer Science Tutors in Miami, Spanish Tutors in Los Angeles, SSAT Tutors in San Francisco-Bay Area

Popular Courses & Classes

SSAT Courses & Classes in Miami, SAT Courses & Classes in San Diego, GRE Courses & Classes in Phoenix, Spanish Courses & Classes in Boston, GMAT Courses & Classes in Miami, GRE Courses & Classes in Philadelphia, ACT Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in Chicago, GMAT Courses & Classes in Los Angeles, SAT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

GMAT Test Prep in Chicago, LSAT Test Prep in Washington DC, ISEE Test Prep in Los Angeles, SAT Test Prep in Dallas Fort Worth, GMAT Test Prep in Washington DC, ACT Test Prep in Atlanta, LSAT Test Prep in New York City, MCAT Test Prep in Atlanta, GRE Test Prep in San Diego, ISEE Test Prep in San Diego

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : How to find an angle in a polygon

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : How To Find An Angle In A Polygon

Example Question #12 : Other Polygons

Example Question #13 : Other Polygons

Example Question #14 : Other Polygons

Example Question #2 : How To Find An Angle In A Polygon

Example Question #2 : How To Find An Angle In A Polygon

Example Question #21 : Geometry

Example Question #5 : How To Find An Angle In A Polygon

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: