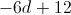High School Math : How to use the distributive property in pre-algebra
Study concepts, example questions & explanations for High School Math
All High School Math Resources
Example Questions
Example Question #1 : How To Use The Distributive Property In Pre Algebra
Simplify the expression.
Use the distributive property to multiply each term of the polynomial by 
Example Question #1 : How To Use The Distributive Property In Pre Algebra
Find the value of 
-2
4
6
2
-6
2
We can seperate the problem into two steps:
We then combine the two parts:
Example Question #1 : Distributive Property
Distribute 
When distributing with negative numbers we must remember to distribute the negative to all of the variables in the parentheses.
Distribute the 
Perform the multiplication remembering the positive/negative rules to get 
Example Question #1 : Distributive Property
Simplify the expression.
Multiply the mononomial by each term in the binomial, using the distributive property.
Example Question #1 : High School Math
Simplify the expression.
Use the distributive property to multiply each term by 
Simplify.
Example Question #1 : High School Math
Simplify the following expression:
Recall that the distributive property requires that we multiply the outside term by both terms in parentheses and add the results.
Example Question #3 : High School Math
Evaluate the following expression:
None of the above
Recall the distributive property. We need to multiply the outside factor by both terms inside and then combine.
Thus,
Example Question #2 : High School Math
Distribute:
When distributing with negative numbers we must remember to distribute the negative to all of the terms in the parentheses.
Remember, a negative multiplied by a negative is positive, and a negative multiplied by a positive number is negative.
Distribute the 
Perform the multiplication, remembering the positive/negative rules:
Example Question #2 : Distributive Property
Which of the following is equivalent to 
We need to distribute -3 by multiplying both terms inside the parentheses by -3.:
Now we can multiply and simplify. Remember that multiplying two negative numbers results in a positive number:
Example Question #3 : Distributive Property
Expand:
Use the distributive property. Do not forget that the negative sign needs to be distributed as well!
Add the terms together:
All High School Math Resources
