All High School Math Resources
Example Questions
Example Question #1 : Functions And Graphs
What is the center and radius of the circle indicated by the equation?
A circle is defined by an equation in the format 
The center is indicated by the point 

In the equation 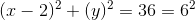


Example Question #1 : Pre Calculus
What is the shape of the graph indicated by the equation?
Circle
Parabola
Hyperbola
Ellipse
Ellipse
An ellipse has an equation that can be written in the format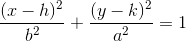
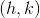

Example Question #1 : Pre Calculus
A conic section is represented by the following equation:
What type of conic section does this equation represent?
Hyperbola
Parabola
Ellipse
Circle
Hyperbola
The simplest way to know what kind of conic section an equation represents is by checking the coefficients in front of each variable. The equation must be in general form while you do this check. Luckily, this equation is already in general form, so it's easy to see. The general equation for a conic section is the following:
Assuming the term 
- If A equals C, the equation is a circle.
- If A and C have the same sign (but are not equal to each other), the equation is an ellipse.
- If either A or C equals 0, the equation is a parabola.
- If A and C are different signs (i.e. one is negative and one is positive), the equation is a hyperbola.
Example Question #1 : Pre Calculus
A conic section is represented by the following equation:
Which of the following best describes this equation?
horizontal hyperbola with center 

vertical parabola with vertex 
horizontal hyperbola with center of 

vertical hyperbola with center 

vertical ellipse with center 
horizontal hyperbola with center of 

First, we need to make sure the conic section equation is in a form we recognize. Luckily, this equation is already in standard form:
The first step is to determine the type of conic section this equation represents. Because there are two squared variables (

In a hyperbola, the squared term with a positive coefficient represents the direction in which the hyperbola opens. In other words, if the 

The center is always found at 

That leaves only the asymptotes. For a hyperbola, the slopes of the asymptotes can be found by dividing 



In this case, 



Example Question #2 : Pre Calculus
Find the vertex 
For any parabola of the form 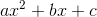
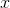
So here, we have
=
We plug this back into the original equation to find 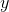
=
Example Question #3 : Pre Calculus
What is the minimal value of
over all real numbers?
No minimum value.
Since this is an upwards-opening parabola, its minimum value will occur at the vertex. The 
is at
So here,
We plug this value back into the equation of the parabola, to find the value of the function at this 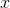
Thus the minimal value of the expression is 
Example Question #2 : Functions And Graphs
The function 
When you take the second derivative of the function 
What can you conclude about the function at 
The point is an absolute minimum.
The point is an inflection point.
The point is a local maximum.
The point is an absolute maximum.
The point is a local minimum.
The point is an inflection point.
We have a point at which 
Plug in 0 into the second derivative to obtain
So the point is an inflection point.
Example Question #2 : Pre Calculus
Consider the function
Find the maximum of the function on the interval ![\left [ 0,1 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/90593/gif.latex)
Notice that on the interval ![\left [ 0,1 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/90594/gif.latex)





Plugging in either 1 or 0 into the original function 
Example Question #3 : Pre Calculus
What is the domain of the function below:
The domain is defined as the set of possible values for the x variable. In order to find the impossible values of x, we should:
a) Set the equation under the radical equal to zero and look for probable x values that make the expression inside the radical negative:
There is no real value for x that will fit this equation, because any real value square is a positive number i.e. cannot be a negative number.
b) Set the denominator of the fractional function equal to zero and look for probable x values:
Now we can solve the equation for x:
There is no real value for x that will fit this equation.
The radical is always positive and denominator is never equal to zero, so the f(x) is defined for all real values of x. That means the set of all real numbers is the domain of the f(x) and the correct answer is 
Alternative solution for the second part of the solution:
After figuring out that the expression under the radical is always positive (part a), we can solve the radical and therefore denominator for the least possible value (minimum value). Setting the x value equal to zero will give the minimum possible value for the denominator.
That means the denominator will always be a positive value greater than 1/2; thus it cannot be equal to zero by setting any real value for x. Therefore the set of all real numbers is the domain of the f(x).
Example Question #1 : Finding Domain And Range
What is the domain of the function below?
The domain is defined as the set of all values of x for which the function is defined i.e. has a real result. The square root of a negative number isn't defined, so we should find the intervals where that occurs:
The square of any number is positive, so we can't eliminate any x-values yet.
If the denominator is zero, the expression will also be undefined.
Find the x-values which would make the denominator 0:
Therefore, the domain is 
Certified Tutor
Certified Tutor
All High School Math Resources





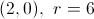









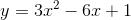



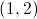
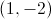
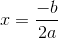






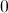



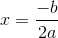




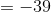




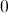


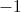
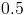
![f(x)=\frac{1}{\sqrt[4]{x^{2}+1}-\frac{1}{2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/138723/gif.latex)




![\sqrt[4]{x^2+1}-\frac{1}{2}=0](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/93233/gif.latex)


![\sqrt[4]{x^2+1}-\frac{1}{2}=](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/93235/gif.latex)
![\sqrt[4]{0+1}-\frac{1}{2}=](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/138727/gif.latex)












