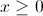All High School Math Resources
Example Questions
Example Question #43 : Basic Single Variable Algebra
Solve for 
Inequalities can be treated like any other equation except when multiplying and dividing by negative numbers. When multiplying or dividing by negative numbers, we just flip the sign of the inequality so that 

Example Question #44 : Basic Single Variable Algebra
Solve for 
Inequalities can be treated like any other equation except when multiplying and dividing by negative numbers. When multiplying or dividing by negative numbers, we just flip the sign of the inequality so that 


So when we solve inequalities with binomials, we must create two scenarios: one where the value inside of the parentheses is positive and one where it is negative. For the negative scenario, we must flip the sign as we normally do for inequalities.
Now we must create our two scenarios:

Notice that in the negative scenario, we flipped the sign of the inequality.


Example Question #45 : Basic Single Variable Algebra
Solve for 
Inequalities can be treated like any other equation except when multiplying and dividing by negative numbers. When multiplying or dividing by negative numbers, we just flip the sign of the inequality so that 


So when we solve inequalities with binomials, we must create two scenarios: one where the value inside of the parentheses is positive and one where it is negative. For the negative scenario, we must flip the sign as we normally do for inequalities.
Now we must create our two scenarios:

Notice that in the negative scenario, we flipped the sign of the inequality.


Example Question #51 : Basic Single Variable Algebra
Solve the inequality for x:
Subtract 4 from both sides:
Divide both sides by 2:
Example Question #231 : Basic Single Variable Algebra
Solve for 
Add 4 to both sides.
Divide both sides by –7. When dividing by a negative value, we must also change the direction of the inequality sign.
Example Question #52 : Basic Single Variable Algebra
Solve for 
Move like terms to the same sides:
Combine like terms:
Divide both sides by 3:
Example Question #53 : Basic Single Variable Algebra
Solve for 
Inequalities can be treated like any other equation except when multiplying and dividing by negative numbers. When multiplying or dividing by negative numbers, we just flip the sign of the inequality so that 

Certified Tutor
Certified Tutor
All High School Math Resources