Polinomios con raíces complejas
El teorema fundamental del Álgebra nos asegura que cualquier polinomio con coeficientes de número real puede factorizarse completamente sobre el campo de los números complejos .
En el caso de los polinomios cuadráticos , las raíces son complejas cuando el discriminante es negativo.
Ejemplo 1:
Factorice completamente, usando números complejos.

Primero, factorice una x .

Ahora use la
fórmula cuadrática
para la expresión dentro del paréntesis, para encontrar los valores de
x
para los cuales
 .
.
Aquí a = 1, b = 10 y c =169.


Escriba la raíz cuadrada usando números imaginarios.

Ahora sabemos que los valores de x para los cuales la expresión

es igual a 0 son
 .
.
Así, el polinomio original puede factorizarse como

Puede verificar esto usando el FOIL .
Algunas veces, puede factorizar un polinomio usando números complejos sin usar la fórmula cuadrática. Por ejemplo, la regla de la diferencia de cuadrados :

Esto también puede ser usado con números complejos cuando
 es negativa, como sigue:
es negativa, como sigue:

Ejemplo 2 :
Factorice completamente, usando números complejos.

Primero, factorice
 .
.

Ahora, use la regla de la diferencia de cuadrados para factorizar
 .
.
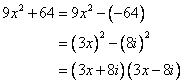
Por lo tanto,
 .
.
- Old French Tutors
- MAP Test Prep
- 2nd Grade Math Tutors
- STAAR Courses & Classes
- CAST Test Tutors
- CCNP - Cisco Certified Network Professional Courses & Classes
- AWS Certified Developer Test Prep
- IB Dance Tutors
- Florida Bar Exam Courses & Classes
- CTP - Certified Treasury Professional Courses & Classes
- Linguistics Tutors
- SSAT- Elementary Level Tutors
- Ohio Bar Exam Test Prep
- Nematology Tutors
- International Sports Sciences Association Courses & Classes
- CMT - Chartered Market Technician Courses & Classes
- OAT Courses & Classes
- GED Tutors
- Typology Tutors
- FRT - Foundations of Reading Test Courses & Classes