Resolviendo sistemas de ecuaciones lineales usando matrices

Si lo necesita, revise las matrices , operaciones de renglones de matrices y resolviendo sistemas de ecuaciones lineales antes de leer esta página.

El métdo de matrices para resolver sistemas de ecuaciones lineales es solo el método de eliminación disfrazado. Al usar matrices, la notación se vuelve un poco más fácil.

Suponga que tiene un sistema de ecuaciones lineales tal como:

El primer paso es convertir esto en una matriz. Asegúrese que todas las ecuaciones estén en la forma estándar ( Ax + B y = C ), y use los coeficientes de cada ecuación para formar cada renglón de la matriz. Puede ayudarle separar la columna de la derecha con una línea punteada.

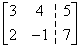
Enseguida, usamos las operaciones de renglones de matrices para cambiar la matriz 2 × 2 en el lado izquierdo a la matriz identidad . Primero, queremos obtener un cero en el Renglón 1, Columna 2. Así, sume 4 por el Renglón 2 al Renglón 1.

Enseguida queremos un 1 en la esquina superior izquierda.

Ahora queremos un cero en la esquina inferior izquierda.

Finalmente, queremos un 1 en el Renglón 2, Columna 2.

Ahora que tenemos la matriz identidad 2 × 2 en la izquierda, podemos leer las soluciones de la columna derecha:

x = 3

y = –1

El mismo método puede ser usado para n ecuaciones lineales en n valores desconocidos; en este caso Usted crearía una matriz n × ( n + 1), y usaría las operaciones de renglones de matrices para obtener la matriz identidad n × n en el lado izquierdo.

Nota importante: Si las ecuaciones representadas por su matriz original representan rectas paralelas, no podrá obtener la matriz identidad usando las operaciones de renglones. En este caso, la solución puede no existir o hay infinitamente muchas soluciones para el sistema.