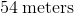The formula for circumference is \(\displaystyle \dpi{100} \pi d\) or \(\displaystyle \dpi{100} 2\pi r\).

Since we are given the radius, we will use \(\displaystyle \dpi{100} 2\pi r\).

\(\displaystyle \dpi{100} 2\pi r=2\pi (5)=10\pi\)

The formula for the perimeter of a square is \(\displaystyle \dpi{100} 4s\), where \(\displaystyle \dpi{100} s\) is the length of one side of the square.

So \(\displaystyle \dpi{100} 4\cdot (4)=16\)

The formula for the perimeter of a rectangle is \(\displaystyle \dpi{100} P=2l+2w\), where \(\displaystyle \dpi{100} l\) is the length of the rectangle and \(\displaystyle \dpi{100} w\) is the width.

Plug in the numbers that we are given into the equation.

\(\displaystyle \dpi{100} 40=2l +2(8)\)

\(\displaystyle \dpi{100} 40=2l +16\)

\(\displaystyle \dpi{100} 40-16=2l +16-16\)

\(\displaystyle \dpi{100} 24=2l\)

\(\displaystyle \dpi{100} \frac{24}{2}=\frac{2l}{2}\)

\(\displaystyle \dpi{100} l=12\)

When searching for the perimeter of a rectangle we are looking for the sum of the lengths of all of the sides enclosing the figure. In this case there are four sides, two that are the base and two that are the height. To find the perimeter we add all four of them together.

Therefore the equation for the perimeter of a rectangle is \(\displaystyle 2(Base)+2(Height)=Perimeter\: of\: a\: Rectangle\)

In this case the equation looks like this \(\displaystyle 2(4)+2(8)\) 

Multiply the numbers together \(\displaystyle 8+16\)

Then add them to get the answer \(\displaystyle 24\)

The perimeter of a rectangle is the sum of four sides, two that are the base and two that are the height. To find the perimeter we add all four of them together.

Therefore the equation for the perimeter of a rectangle is

In this example we plug in the base and the perimeter so the equation looks like this \(\displaystyle 2(Height)+2(12)=30\)

Perform the multiplication to get \(\displaystyle 2(Height)+24=30\)

Subtract from both sides to arrive at  \(\displaystyle 2(Height)=6\)

Then divide by 2 to find the height \(\displaystyle \frac{2(Height)}{2}=\frac{6}{2}\)

The answer \(\displaystyle Height=3\)

When searching for the perimeter of a square we are looking for the sum of the lengths of all of the sides enclosing the figure. In this case there are four sides that are all equal length. To find the perimeter we add all four of them together or multiply the side length by four.

In this example the equation looks like this:

\(\displaystyle Perimeter\: of\: square=4*8\)

Multiply the numbers together to get \(\displaystyle 32\).

To find the radius of a circle given the circumference we must first know the equation for the circumference of a circle which is 

\(\displaystyle Circumference=2\pi(r)\)

Then we plug in the circumference into the equation for \(\displaystyle C\) yielding \(\displaystyle 64\pi=2\pi(r)\)

We then divide each side by \(\displaystyle 2\pi\): \(\displaystyle \frac{64\pi}{2\pi}=32\)

We then have the answer for \(\displaystyle r\) which is \(\displaystyle 32\).

We define the variables as \(\displaystyle w = \mbox{width}\) and \(\displaystyle l = \mbox{length} = w + 2\).

We substitute these values into the equation for the area of a rectangle and get \(\displaystyle A_{\mbox{rectangle} }= wl = w(w + 2) = 80\). 

\(\displaystyle w^2 +2w-80=0\)

\(\displaystyle (w - 8)(w + 10) = 0\)

\(\displaystyle w = 8\) or \(\displaystyle w = -10\)

Lengths cannot be negative, so the only correct answer is \(\displaystyle w = 8\). If \(\displaystyle w = 8\), then \(\displaystyle l = 10\). 

Therefore, \(\displaystyle \mbox{perimeter }= 2w + 2l = 16 + 20 = 36\:\mbox{m}\).

To find the perimeter of the square, find the length of the side.  Write the formula to find the length of the side.

\(\displaystyle d=\sqrt{s^2+s^2}\)

Substitute the diagonal and solve for the side.

\(\displaystyle \sqrt2=\sqrt{s^2+s^2}\) 

First, square each side to get rid of the square root. 

\(\displaystyle 2=2s^2\)

Divide 2 by each side to isolate the \(\displaystyle s^2\)

\(\displaystyle 1=s^2\)

Take the square root of each side.

\(\displaystyle 1=s\)

Since there are four sides in a square, multiply the side length by four to get the perimeter.

\(\displaystyle P=4(1)=4\)

The perimeter of an equilateral triangle is three times the length of its side.

\(\displaystyle P=3(-x-4) = -3x-12\)