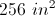All Intermediate Geometry Resources
Example Questions
Example Question #41 : Parallelograms
The perimeter of a square is 
The perimeter of a square is geven by 

Thus
so 
The original side is reduced by a factor of 

Example Question #1 : How To Find The Area Of A Parallelogram
Find the area of the box in square inches:

The answer is 
Foil
If you chose 
Just remember, the width is 12 added to 

Example Question #42 : Parallelograms
If all angles are right angles in the figure below, what is the total area of the figure?

The answer is 
To get the area, you would need to find the missing sides. Since the horizontal top is 



The vertical right side is 


Then you would have to split the figure into 3 different boxes and find the area of each one. Then you would add the area of each box
Example Question #1 : How To Find The Area Of A Parallelogram
What is the area of a parallelogram if the base is 

The formula for the area of a parallelogram is:
So, we are given all of the information that we need to solve this problem. Substitute the provided values into the equation and simplify:
Example Question #1 : How To Find The Area Of A Parallelogram
What is the area of a parallelogram if the base is 

The formula for the area of a parallelogram is:
Substitute in the provided values and simplify to calculate the correct answer:
Example Question #219 : Quadrilaterals
Find the area of a parallelogram if the base is 

The formula for the area of a parallelogram is:
Substitute the values provided in the question:
Use the FOIL method to simplify:
Example Question #220 : Quadrilaterals
What is the area of a parallelogram if the base is 

The formula for the area of a parallelogram is:
Substitute the values provided in the problem and solve to calculate the correct answer:
Example Question #1 : How To Find The Area Of A Parallelogram
If the height of the parallelogram is half of the length of the rectangle, then find the area of the shaded region in the figure.


In order to find the area of the shaded region, we must first find the areas of the rectangle and parallelogram.
Recall how to find the area of a rectangle:
Substitute in the given length and height to find the area of the rectangle.
Next, find the area of the parallelogram.
Recall how to find the area of a parallelogram:
We need to find the height of the parallelogram. From the question, we know the following relationship:
Substitute in the length of the rectangle to find the height of the parallelogram.
Now, substitute in the height and the given length of the base to find the area of the parallelogram.
Now, we are ready to find the area of the shaded region by subtracting the area of the parallelogram from the area of the rectangle.
Solve.
Example Question #2 : How To Find The Area Of A Parallelogram
If the height of the parallelogram is half of the length of the rectangle, then find the area of the shaded region in the figure.


In order to find the area of the shaded region, we must first find the areas of the rectangle and parallelogram.
Recall how to find the area of a rectangle:
Substitute in the given length and height to find the area of the rectangle.
Next, find the area of the parallelogram.
Recall how to find the area of a parallelogram:
We need to find the height of the parallelogram. From the question, we know the following relationship:
Substitute in the length of the rectangle to find the height of the parallelogram.
Now, substitute in the height and the given length of the base to find the area of the parallelogram.
Now, we are ready to find the area of the shaded region by subtracting the area of the parallelogram from the area of the rectangle.
Solve.
Example Question #3 : How To Find The Area Of A Parallelogram
If the height of the parallelogram is half of the length of the rectangle, then find the area of the shaded region in the figure.


In order to find the area of the shaded region, we must first find the areas of the rectangle and parallelogram.
Recall how to find the area of a rectangle:
Substitute in the given length and height to find the area of the rectangle.
Next, find the area of the parallelogram.
Recall how to find the area of a parallelogram:
We need to find the height of the parallelogram. From the question, we know the following relationship:
Substitute in the length of the rectangle to find the height of the parallelogram.
Now, substitute in the height and the given length of the base to find the area of the parallelogram.
Now, we are ready to find the area of the shaded region by subtracting the area of the parallelogram from the area of the rectangle.
Solve.
Certified Tutor
All Intermediate Geometry Resources