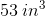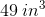All ISEE Upper Level Math Resources
Example Questions
Example Question #1 : How To Find The Volume Of A Cube
If a cube is 
Not enough information provided.
To find the volume of a cube, we multiply length by width by height, which can be represented with the forumla 

Example Question #1 : How To Find The Volume Of A Cube
What is the volume of a cube with a side length equal to 
The volume of a a cube (or rectangular prism) can be solved using the following equation:
Example Question #2 : How To Find The Volume Of A Cube
Give the volume of a cube with surface area 150 square inches.
Let 



The volume is the cube of this, or 
Example Question #1 : How To Find The Volume Of A Cube
What is the volume of a cube in which the edge is equal to ![\sqrt[3]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/200393/gif.latex)

First, the value of x must be solved for:
Given the edge of the cube is ![\sqrt[3]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/200399/gif.latex)
![\sqrt[3]{62}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/200400/gif.latex)
Thus, 62 is the correct answer.
Example Question #3 : Cubes
The length of a diagonal of one face of a cube is 
Since a diagonal of a square face of the cube is

Cube this to get the volume of the cube:
Example Question #1 : Cubes
The distance from one vertex of a perfectly cubic aquarium to its opposite vertex is 1.5 meters. Give the volume of the aquarium in liters.
1 cubic meter = 1,000 liters.
The correct answer is not given among the other responses.
The correct answer is not given among the other responses.
Let 

Cube this sidelength to get the volume:

To convert this to liters, multiply by 1,000:

This is not among the given responses.
Example Question #2 : How To Find The Volume Of A Cube
Give the volume of a cube with surface area 240 square inches.
Let 



The volume is the cube of this, or 
Example Question #3 : How To Find The Volume Of A Cube
An aquarium is shaped like a perfect cube; the perimeter of each glass face is 

Insufficient information is given to answer the question.
Note:
A perfect cube has square faces; if a face has perimeter 


Its capacity in liters is 


This rounds to
Example Question #3 : How To Find The Volume Of A Cube
Your friend gives you a puzzle cube for your birthday. If the length of one edge is 5cm, what is the volume of the cube?
Your friend gives you a puzzle cube for your birthday. If the length of one edge is 5cm, what is the volume of the cube?
To find the volume of a cube, use the following formula:
Where s is the side length.
Plug in what we know to get our answer:
Example Question #331 : Isee Upper Level (Grades 9 12) Mathematics Achievement
A cube has a side length of 
A cube has a side length of 
To find the volume of a cube, use the following formula:
Plug in our known side length and solve
Making our answer:
All ISEE Upper Level Math Resources