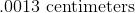All New SAT Math - Calculator Resources
Example Questions
Example Question #1 : Conversions
How many 
To solve this problem we can make proportions.
We know that 
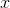
Next, we want to cross multiply and divide to isolate the on one side.
The 
Example Question #2 : Conversions
How many 
To solve this problem we can make proportions.
We know that 

Next, we want to cross multiply and divide to isolate the on one side.
The 
Example Question #1 : Solving Word Problems With One Unit Conversions
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
Reduce.
The carpenter needs 
Example Question #3 : Conversions
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
Reduce.
The carpenter needs 
Example Question #2 : Solving Word Problems With One Unit Conversions
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
Reduce.
The carpenter needs 
Example Question #81 : New Sat Math Calculator
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
Reduce.
The carpenter needs 
Example Question #3 : Solving Word Problems With One Unit Conversions
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
The carpenter needs 


Example Question #2101 : Psat Mathematics
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
Reduce.
The carpenter needs 
Example Question #4 : Conversions
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
The carpenter needs 
Example Question #4 : Solving Word Problems With One Unit Conversions
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
Reduce.
The carpenter needs 
Certified Tutor
Certified Tutor
All New SAT Math - Calculator Resources