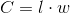Call Now to Set Up Tutoring:

(888) 888-0446

Pre-Algebra : Perimeter

Study concepts, example questions & explanations for Pre-Algebra

Create An Account

All Pre-Algebra Resources

11 Diagnostic Tests 177 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Perimeter

Becky's house is surrounded by a circular lake that Becky runs around each day. If Becky wants to figure out the distance she runs around the lake, what formula should Becky use?

Possible Answers:

$C=l\cdot w$ $\displaystyle C=l\cdot w$

None of the other answers

$C=2\Pi r$ $\displaystyle C=2\Pi r$

$C=\Pi r^{2}$ $\displaystyle C=\Pi r^{2}$

$P=d\Pi$ $\displaystyle P=d\Pi$

Correct answer:

$C=2\Pi r$ $\displaystyle C=2\Pi r$

Explanation:

Becky should use the circumfrence formula to find the distance she runs of a lake.

Correct Answer: $C=2\Pi r$ $\displaystyle C=2\Pi r$

Report an Error

Example Question #2 : Perimeter

What is the circumference of a circle with an area equal to $81\pi$ $\displaystyle 81\pi$?

Possible Answers:

$36\pi$ $\displaystyle 36\pi$

$4.5\pi$ $\displaystyle 4.5\pi$

$18\pi$ $\displaystyle 18\pi$

$9\pi$ $\displaystyle 9\pi$

Correct answer:

$18\pi$ $\displaystyle 18\pi$

Explanation:

Using the area, solve for the radius:

$A=r^2\pi$ $\displaystyle A=r^2\pi$

$81\pi=r^2\pi$ $\displaystyle 81\pi=r^2\pi$

Divide by $\pi$ $\displaystyle \pi$:

81=r^2 $\displaystyle 81=r^2$

Take the square root:

$\sqrt{81}=9=r$ $\displaystyle \sqrt{81}=9=r$

Plug this radius into the formula for the circumference:

$C=2r\pi=2(9)\pi=18\pi$ $\displaystyle C=2r\pi=2(9)\pi=18\pi$

Report an Error

Example Question #1 : Circumference Of A Circle

What is the circumference of a circle with a radius equal to $\displaystyle 7$?

Possible Answers:

$196\pi$ $\displaystyle 196\pi$

$7\pi$ $\displaystyle 7\pi$

$49\pi$ $\displaystyle 49\pi$

$14\pi$ $\displaystyle 14\pi$

Correct answer:

$14\pi$ $\displaystyle 14\pi$

Explanation:

The circumference can be solved using the following equation:

$C=2r\pi=2(7)\pi=14\pi$ $\displaystyle C=2r\pi=2(7)\pi=14\pi$

Report an Error

Example Question #1 : Circumference Of A Circle

What is the circumference of a circle with a radius of $\displaystyle 8$?

Possible Answers:

$\displaystyle 16$

$16\pi$ $\displaystyle 16\pi$

$16\pi^{2}$ $\displaystyle 16\pi^{2}$

$28\pi$ $\displaystyle 28\pi$

$8\pi$ $\displaystyle 8\pi$

Correct answer:

$16\pi$ $\displaystyle 16\pi$

Explanation:

The circumference can be solved using the following equation:

$C=2r\pi$ $\displaystyle C=2r\pi$

Where $\displaystyle r$ represents the radius. Therefore, when we substitute our radius in we get:

$=2(8)\pi =16\pi$ $\displaystyle =2(8)\pi =16\pi$

Report an Error

Example Question #1 : Know And Use The Formulas For The Area And Circumference Of A Circle: Ccss.Math.Content.7.G.B.4

The perimeter of a given rectangle is equal to the circumference of a given circle. The circle has radius $\displaystyle 30$ inches; the width of the rectangle is $8 \pi$ $\displaystyle 8 \pi$ inches. What is the length of the rectangle?

Possible Answers:

$7\pi$ $\displaystyle 7\pi$ inches

$(30 - 8 \pi )$ $\displaystyle (30 - 8 \pi )$ inches

$14 \pi$ $\displaystyle 14 \pi$ inches

$44 \pi$ $\displaystyle 44 \pi$ inches

$22 \pi$ $\displaystyle 22 \pi$ inches

Correct answer:

$22 \pi$ $\displaystyle 22 \pi$ inches

Explanation:

The circumference of a circle with radius $\displaystyle 30$ inches is

$C = 2 \pi r = 2 \pi \cdot 30 = 60 \pi$ $\displaystyle C = 2 \pi r = 2 \pi \cdot 30 = 60 \pi$ inches.

The perimeter of the rectangle is therefore $60 \pi$ $\displaystyle 60 \pi$ inches. To find its length, substitute $W = 8\pi$ $\displaystyle W = 8\pi$ and $P = 60\pi$ $\displaystyle P = 60\pi$ into the equation and solve for $\displaystyle L$:

$\displaystyle 2 L + 2W = P$

$2 L + 2 \cdot 8 \pi = 60 \pi$ $\displaystyle 2 L + 2 \cdot 8 \pi = 60 \pi$

$2 L + 16 \pi = 60 \pi$ $\displaystyle 2 L + 16 \pi = 60 \pi$

$2 L + 16 \pi - 16 \pi = 60 \pi - 16 \pi$ $\displaystyle 2 L + 16 \pi - 16 \pi = 60 \pi - 16 \pi$

$2 L =44 \pi$ $\displaystyle 2 L =44 \pi$

$2 L \div 2=44 \pi \div 2$ $\displaystyle 2 L \div 2=44 \pi \div 2$

$L = 22\pi$ $\displaystyle L = 22\pi$ inches

Report an Error

Example Question #3 : Perimeter

Determine the circumference of the circle if the radius is 20.

Possible Answers:

$400\pi$ $\displaystyle 400\pi$

$20\pi$ $\displaystyle 20\pi$

$200\pi$ $\displaystyle 200\pi$

$80\pi$ $\displaystyle 80\pi$

$40\pi$ $\displaystyle 40\pi$

Correct answer:

$40\pi$ $\displaystyle 40\pi$

Explanation:

Write the formula for circumference.

$C=2\pi r$ $\displaystyle C=2\pi r$

Substitute the radius and solve.

$C=2\pi(20) = 40\pi$ $\displaystyle C=2\pi(20) = 40\pi$

Report an Error

Example Question #3 : Circumference Of A Circle

Given the area of the circle is $9\pi$ $\displaystyle 9\pi$, what is the circumference of the circle?

Possible Answers:

$\displaystyle 3$

$6\pi +6$ $\displaystyle 6\pi +6$

$\displaystyle 9$

$3+3\pi$ $\displaystyle 3+3\pi$

$6\pi$ $\displaystyle 6\pi$

Correct answer:

$6\pi$ $\displaystyle 6\pi$

Explanation:

Write the formula for the area of a circle.

$A=\pi r^2$ $\displaystyle A=\pi r^2$

Substitute the area.

$9\pi=\pi r^2$ $\displaystyle 9\pi=\pi r^2$

r^2=9 $\displaystyle r^2=9$

r=3 $\displaystyle r=3$

Write the circumference of the circle.

$C=2\pi r$ $\displaystyle C=2\pi r$

Substitute the radius.

$C=2\pi (3) = 6\pi$ $\displaystyle C=2\pi (3) = 6\pi$

Report an Error

Example Question #271 : Geometry

Find the circumference of a circle with an area of $\pi^2$ $\displaystyle \pi^2$.

Possible Answers:

$2\pi ^3$ $\displaystyle 2\pi ^3$

$2\pi \sqrt{\pi}$ $\displaystyle 2\pi \sqrt{\pi}$

$\pi \sqrt{\pi}$ $\displaystyle \pi \sqrt{\pi}$

$3\pi$ $\displaystyle 3\pi$

$3\pi^2$ $\displaystyle 3\pi^2$

Correct answer:

$2\pi \sqrt{\pi}$ $\displaystyle 2\pi \sqrt{\pi}$

Explanation:

Write the area formula in order to find the radius.

$A=\pi r^2$ $\displaystyle A=\pi r^2$

Substitute the area.

$\pi ^2=\pi r^2$ $\displaystyle \pi ^2=\pi r^2$

$r^2=\pi$ $\displaystyle r^2=\pi$

$r=\sqrt{\pi}$ $\displaystyle r=\sqrt{\pi}$

Write the circumference formula.

$C=2\pi r$ $\displaystyle C=2\pi r$

Substitute the radius.

$C=2\pi \sqrt{\pi}$ $\displaystyle C=2\pi \sqrt{\pi}$

Report an Error

Example Question #4 : Perimeter

Determine the circumference of the circle if the radius is $2\pi$ $\displaystyle 2\pi$.

Possible Answers:

$4\pi ^2$ $\displaystyle 4\pi ^2$

$8\pi$ $\displaystyle 8\pi$

$2\pi ^2$ $\displaystyle 2\pi ^2$

$4\pi ^3$ $\displaystyle 4\pi ^3$

$4\pi$ $\displaystyle 4\pi$

Correct answer:

$4\pi ^2$ $\displaystyle 4\pi ^2$

Explanation:

Write the formula for the circumference of a circle.

$C=2\pi r$ $\displaystyle C=2\pi r$

Substitute the radius into the formula.

$C=2\pi (2\pi) = 4\pi ^2$ $\displaystyle C=2\pi (2\pi) = 4\pi ^2$

Report an Error

Example Question #5 : Perimeter

Find the circumference of a circle with a radius of $\sqrt2$ $\displaystyle \sqrt2$.

Possible Answers:

$\frac{\sqrt2}{2} \pi$ $\displaystyle \frac{\sqrt2}{2} \pi$

$2\pi$ $\displaystyle 2\pi$

$\frac{\sqrt{2\pi}}{2}$ $\displaystyle \frac{\sqrt{2\pi}}{2}$

$4\pi$ $\displaystyle 4\pi$

$2\pi \sqrt{2}$ $\displaystyle 2\pi \sqrt{2}$

Correct answer:

$2\pi \sqrt{2}$ $\displaystyle 2\pi \sqrt{2}$

Explanation:

Write the formula to find the circumference of a circle.

$C=2\pi r$ $\displaystyle C=2\pi r$

Substitute the radius.

$C=2\pi \sqrt{2}$ $\displaystyle C=2\pi \sqrt{2}$

Report an Error

View Pre-Algebra Tutors

Louis
Certified Tutor

University of California-Los Angeles, Bachelor in Arts, Film Production.

View Pre-Algebra Tutors

Joshua
Certified Tutor

Brigham Young University - Idaho, Bachelor, Mathematical Sciences.

View Pre-Algebra Tutors

George
Certified Tutor

Colby College, Bachelors, Economics/Spanish. Massachusetts Institute of Technology, Masters, Urban Studies.

All Pre-Algebra Resources

11 Diagnostic Tests 177 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in Dallas Fort Worth, Chemistry Tutors in San Diego, Physics Tutors in Phoenix, Statistics Tutors in San Diego, Statistics Tutors in Houston, English Tutors in Washington DC, ISEE Tutors in San Diego, Computer Science Tutors in Dallas Fort Worth, Algebra Tutors in Boston, English Tutors in Chicago

Popular Courses & Classes

Spanish Courses & Classes in Miami, LSAT Courses & Classes in Houston, GMAT Courses & Classes in Atlanta, LSAT Courses & Classes in Philadelphia, MCAT Courses & Classes in Atlanta, ISEE Courses & Classes in Washington DC, LSAT Courses & Classes in Miami, ACT Courses & Classes in Phoenix, ISEE Courses & Classes in Phoenix, GMAT Courses & Classes in Dallas Fort Worth

Popular Test Prep

SSAT Test Prep in Los Angeles, LSAT Test Prep in Boston, LSAT Test Prep in Washington DC, ISEE Test Prep in Chicago, MCAT Test Prep in Houston, LSAT Test Prep in Atlanta, MCAT Test Prep in Washington DC, SAT Test Prep in Phoenix, GMAT Test Prep in Dallas Fort Worth, MCAT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Pre-Algebra : Perimeter

Study concepts, example questions & explanations for Pre-Algebra

All Pre-Algebra Resources

Example Questions

Example Question #1 : Perimeter

Example Question #2 : Perimeter

Example Question #1 : Circumference Of A Circle

Example Question #1 : Circumference Of A Circle

Example Question #1 : Know And Use The Formulas For The Area And Circumference Of A Circle: Ccss.Math.Content.7.G.B.4

Example Question #3 : Perimeter

Example Question #3 : Circumference Of A Circle

Example Question #271 : Geometry

Example Question #4 : Perimeter

Example Question #5 : Perimeter

All Pre-Algebra Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: