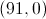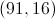Pre-Algebra : Graphing Lines
Study concepts, example questions & explanations for Pre-Algebra
All Pre-Algebra Resources
Example Questions
Example Question #2 : How To Identify A Point In Pre Algebra
What is the slope of the line with the equation 
In the standard form equation of a line, 
In this case the line 
Therefore the answer is 
Example Question #1 : Graphing Lines
What is the slope of the line that contains the points
To find the slope of a line with two points you must properly plug the points into the slope equation for two points which is
We must then properly assign the points to the equation as 
In this case we will make 
Plugging the points into the equation yields
Perform the math to arrive at
The answer is 
Example Question #3 : Graphing Lines
What is the slope of the line 
In the standard form of a line 
In this case the line 
The answer is 
Example Question #4 : Graphing Lines
The equation of a line is 
What are the slope and the y-intercept?
Slope:
y-intercept:
Slope:
y-intercept:
Slope:
y-intercept:
Slope:
y-intercept:
Slope:
y-intercept:
The equation of the line is written in slope-intercept form, 
Example Question #5 : Graphing Lines
What is the y-intercept of the line 
The y-intercept is the point at which the line intersects the y-axis.
It does this at 
We plug 
Anything multiplied by 
Our coordinates for the y-intercept are 
Example Question #6 : Graphing Lines
What is the slope of the line 
In the slope-intercept form of a line,
In this case the line
has a slope of 
The answer is 
Example Question #7 : Graphing Lines
What is the y-intercept of the line 
In the slope-intercept form of a line, 
It does this at
So we plug
to give us
Anything multiplied by
Our coordinates for the y-intercept are 
Example Question #8 : Graphing Lines
What is the slope of a line that is parallel to 
Parallel lines have the same slope.
If an equation is in slope-intercept form, 
In this case 
The slope of our parallel line is 
Example Question #9 : Graphing Lines
What is the slope of the line that contains the points, 
To find the slope of a line with two points you must properly plug the points into the slope equation for two points which looks like
We must then properly assign the points to the equation as
In this case we will make 
Plugging the points into the equation yields
Perform the math to arrive at
The answer is 
Example Question #10 : Graphing Lines
What is the slope of the line that contains the points, 
To find the slope of a line with two points you must properly plug the points into the slope equation for two points which looks like
We must then properly assign the points to the equation as
In this case we will make 
Plugging the points into the equation yields
Perform the math to arrive at
The answer is 
All Pre-Algebra Resources
