All Precalculus Resources
Example Questions
Example Question #1 : Exponential And Logarithmic Functions
You are given that 

Which of the following is equal to 
Since 


Example Question #111 : Pre Calculus
Solve.
None of the other answers
First we condense the LHS to 



Example Question #1 : Exponential And Logarithmic Functions
Solve.
None of the other answers
First take the logarithm of both sides. This yields 






Example Question #1 : Logarithmic Functions
Evalute the equation 
First, we rewrite the equation in logarithmic form to obtain 
Example Question #1 : Logarithmic Functions
Simplify
Example Question #1 : Exponential And Logarithmic Functions
Solve the following equation for 
Logs must be used to solve this problem. Follow the steps below:
Example Question #3 : Exponential And Logarithmic Functions
Solve.
First we condense the LHS to 







Example Question #2 : Exponential And Logarithmic Functions
Find the domain of the function 

The logarithmic function is undefined when the inputs are negative or 0. Therefore the inputs of the logarithmic function must be positive. This means that the quantity 
Therefore the domain of the function 


Example Question #9 : Logarithmic Functions
Use the logarithmic base change formula to convert 

Here we employ the use of the logarithm base change formula

Therefore we get,
Example Question #10 : Logarithmic Functions
Find the domain of the function 
The logarithmic function is undefined when the inputs are negative or 0. Therefore the inputs of the logarithmic function must be positive. This means that the quantity 
Therefore the domain of the function 
![(-\infty,-2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/225450/gif.latex)
Certified Tutor
All Precalculus Resources

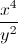

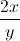

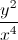





























































![(-\infty,2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/225429/gif.latex)

![(-\infty,-2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/225425/gif.latex)








