To find discontinuity we need to look at where the denominator of the function is equal to zero. Looking at our function,

we need to set the denominator equal to zero and solve for :

When ,  which is undefined.

Therefore  is where the function is discontinuous.

Means to find the limit of the function as  approaches  from the left. We can see that  is a vertical asymptote therefore we need to look at numbers extremely close to zero on the left side. The value of  continues to decrease to the left of zero, with the value of  decreasing even more as  gets closer to . Thus, the limit is 

We first need to simplify the function, we can do this by factoring the numerator and denominator.

If we plug in 3 into the simplified function, we get:

Substituting  in for  we get the following:

When evaluating limits at infinity there are three rules to keep in mind:

1. If the degree of the highest exponent in the numerator is equal to the degree of the highest exponent in the denominator, then the limit is equal to the ratio of the coefficient of the highest exponent in the numerator over the coefficient of the highest exponent in the denominator. Make sure to include signs. 
2. If the degree of the highest exponent in the numerator is less than the degree of the highest exponent in the denominator, the limit = 0.
3. If the degree of the highest exponent in the numerator is greater than the degree of the higest exponent in the denominator, divide the highest power in the numerator by the highest power in the denominator and substitute for inifity. You will either subsitute for positive or negative infinity based on what the questions asks you to evaluate the limit at. 

In this case, the degree is higher in the numerator than the denominator (rule #3). Hence, you need to divide the highest powers and evaluate.

Evaluate  as x:

Answer: limit = 

When evaluating limits at infinity there are three rules to keep in mind:

1. If the degree of the highest exponent in the numerator is equal to the degree of the highest exponent in the denominator, then the limit is equal to the ratio of the coefficient of the highest exponent in the numerator over the coefficient of the highest exponent in the denominator. Make sure to include signs. 
2. If the degree of the highest exponent in the numerator is less than the degree of the highest exponent in the denominator, the limit = 0.
3. If the degree of the highest exponent in the numerator is greater than the degree of the higest exponent in the denominator, divide the highest power in the numerator by the highest power in the denominator and substitute for inifity. You will either subsitute for positive or negative infinity based on what the questions asks you to evaluate the limit at. 

In this case, the both the numerator and denominator have the highest degree of an exponent of 4 (rule #1). Hence, you need to compare the ratio of the coefficients. 

Answer: limit = 

The end behavior of the function  follows the highest powers in both the numerator and denominator. Therefore, to find the limit we need to look only at the term:  as those are the highest powers in the numerator and demoninator.

Now we take the

.

Thus the limit of our original function is also .

 will approach when approaches , so  will be of type  as shown below:

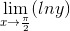
So, we can apply the L’ Hospital's Rule:

since:

hence:

When x=3/2 our denominator is zero so we can't just plug in 3/2 to get our limit. If we look at the numerator when x=3/2 we find that it is zero as well so our numerator can be factored. We see that our limit can be re-written as:

we then can cancel the 2x-3 from the numerator and denominator leaving us with:

and we can just plug in 3/2 into this limit to get 

note: our function is not continuous at x=3/2 but the limit does exist.

To solve this problem we need to expand the term in the numerator 

when we do that we get 

the second degree x terms cancel and we get

now we can cancel our h's in the numerator and denominator to get

then we can just plug 0 in for h and we get our answer