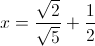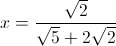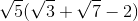\(\displaystyle x\sqrt{45}+x\sqrt{72}=\sqrt{18}\)

Notice how all of the quantities in square roots are divisible by 9

\(\displaystyle x\sqrt{9\times 5}+x\sqrt{9\times 8}=\sqrt{9\times 2}\)

\(\displaystyle x\sqrt{9}\sqrt{5}+x\sqrt{9}\sqrt{4\times 2}=\sqrt{9}\sqrt{2}\)

\(\displaystyle 3x\sqrt{5}+3x\sqrt{4}\sqrt{2}=3\sqrt{2}\)

\(\displaystyle 3x\sqrt{5}+6x\sqrt{2}=3\sqrt{2}\)

\(\displaystyle x(3\sqrt{5}+6\sqrt{2})=3\sqrt{2}\)

\(\displaystyle x=\frac{3\sqrt{2}}{3\sqrt{5}+6\sqrt{2}}\)

Simplifying, this becomes

\(\displaystyle x=\frac{\sqrt{2}}{\sqrt{5}+2\sqrt{2}}\)

\(\displaystyle x\sqrt{72}+x\sqrt{108}=12\)

Note that all of the square root terms share a common factor of 36, which itself is a square of 6:

\(\displaystyle x\sqrt{36\times 2}+x\sqrt{36\times 3}=12\)

\(\displaystyle 6x\sqrt{2}+6x\sqrt{3}=12\)

Factoring \(\displaystyle 6x\) from both terms on the left side of the equation:

\(\displaystyle 6x(\sqrt{2}+\sqrt{3})=12\)

\(\displaystyle 6x=\frac{12}{\sqrt{2}+\sqrt{3}}\)

\(\displaystyle x=\frac{2}{\sqrt{2}+\sqrt{3}}\)

\(\displaystyle 2x\sqrt{12}+3x\sqrt{28}=18\)

Note that both \(\displaystyle \sqrt{12}\) and \(\displaystyle \sqrt{28}\) have a common factor of \(\displaystyle 4\) and \(\displaystyle 4\) is a perfect square:

\(\displaystyle 2x\sqrt{4\times 3}+3x\sqrt{4\times 7}=18\)

\(\displaystyle 2x\cdot2 \sqrt3 +3x\cdot2\sqrt7=18\)

\(\displaystyle 4x\sqrt{3}+6x\sqrt{7}=18\)

From here, we can factor \(\displaystyle 2x\) out of both terms on the lefthand side 

\(\displaystyle 2x(2\sqrt{3}+3\sqrt{7})=18\)

\(\displaystyle 2x(2\sqrt{3}+3\sqrt{7})=18\)

\(\displaystyle x=\frac{18}{2(2\sqrt{3}+3\sqrt{7})}\)

\(\displaystyle x=\frac{9}{2\sqrt{3}+3\sqrt{7}}\)

In order to solve for \(\displaystyle x\), first note that all of the square root terms on the left side of the equation have a common factor of 9 and 9 is a perfect square:

\(\displaystyle x\sqrt{27} + \sqrt{63}=9\)

\(\displaystyle x\sqrt{9\times 3} + \sqrt{9\times 7}=9\)

\(\displaystyle 3x\sqrt{3} + 3\sqrt{7}=9\)

Simplifying, this becomes:

\(\displaystyle 3(x\sqrt{3} + \sqrt{7})=9\)

\(\displaystyle x\sqrt{3} + \sqrt{7}=3\)

\(\displaystyle x\sqrt{3} =3 -\sqrt{7}\)

\(\displaystyle x =\frac{3 -\sqrt{7}}{\sqrt{3}}\)

To begin with, factor out the contents of the radicals.  This will make answering much easier:

\(\displaystyle \sqrt{210}+\sqrt{55}=\sqrt{2*3*5*7}+\sqrt{5*11}\)

They both have a common factor \(\displaystyle 5\).  This means that you could rewrite your equation like this:

\(\displaystyle \sqrt{5}\sqrt{2*3*7}+\sqrt{5}\sqrt{11}\)

This is the same as:

\(\displaystyle \sqrt{5}\sqrt{42}+\sqrt{5}\sqrt{11}\)

These have a common \(\displaystyle \sqrt{5}\).  Therefore, factor that out:

\(\displaystyle \sqrt{5}\sqrt{42}+\sqrt{5}\sqrt{11}=\sqrt{5}(\sqrt{42}+\sqrt{11})\)

These three roots all have a \(\displaystyle 5\) in common; therefore, you can rewrite them:

\(\displaystyle \sqrt{15}-\sqrt{20}+\sqrt{35}=\sqrt{3*5}-\sqrt{4*5}+\sqrt{7*5}\)

Now, this could be rewritten:

\(\displaystyle \sqrt{3*5}-\sqrt{4*5}+\sqrt{7*5}=\sqrt{5}\sqrt{3}-\sqrt{5}\sqrt{4}+\sqrt{5}\sqrt{7}\)

Now, note that \(\displaystyle \sqrt{4}=2\)

Therefore, you can simplify again:

\(\displaystyle \sqrt{5}\sqrt{3}-\sqrt{5}\sqrt{4}+\sqrt{5}\sqrt{7}=\sqrt{5}\sqrt{3}-2\sqrt{5}+\sqrt{5}\sqrt{7}\)

Now, that looks messy! Still, if you look carefully, you see that all of your factors have \(\displaystyle \sqrt{5}\); therefore, factor that out:

\(\displaystyle \sqrt{5}\sqrt{3}-2\sqrt{5}+\sqrt{5}\sqrt{7}=\sqrt{5}(\sqrt{3}-2+\sqrt{7})\)

This is the same as:

\(\displaystyle \sqrt{5}(\sqrt{3}+\sqrt{7}-2)\)

Examining the terms underneath the radicals, we find that \(\displaystyle 128\) and \(\displaystyle 192\) have a common factor of \(\displaystyle 64\). \(\displaystyle 64\) itself is a perfect square, being the product of \(\displaystyle 8\) and \(\displaystyle 8\). Hence, we recognize that the radicals can be re-written in the following manner:

\(\displaystyle \sqrt{128}=\sqrt{64} \sqrt{2}\), and \(\displaystyle \sqrt{192}=\sqrt{64} \sqrt{3}\).

The equation can then be expressed in terms of these factored radicals as shown:

\(\displaystyle 2x\sqrt{128}-3x\sqrt{192}=16\) 

\(\displaystyle \Rightarrow 2x(\sqrt64 \sqrt2)-3x(\sqrt{64} \sqrt3)=16\)  

\(\displaystyle \Rightarrow 2x(8)\sqrt2-3x(8)\sqrt3=16\)

\(\displaystyle \Rightarrow 16x\sqrt2-24x\sqrt3=16\)

Factoring the common term \(\displaystyle 8x\) from the lefthand side of this equation yields

\(\displaystyle 8x (2\sqrt2-3x\sqrt3)=16\)

Divide both sides by the expression in the parentheses:

\(\displaystyle 8x=\frac{16}{2\sqrt2-3x\sqrt3}\)

Divide both sides by \(\displaystyle 8\) to yield \(\displaystyle x\) by itself on the lefthand side:

\(\displaystyle x=\frac{16}{8(2\sqrt2-3x\sqrt3)}\)

Simplify the fraction on the righthand side by dividing the numerator and denominator by \(\displaystyle 8\):

\(\displaystyle x=\frac{2}{2\sqrt{2}-3\sqrt{3}}\)

This is the solution for the unknown variable \(\displaystyle x\) that we have been required to find.