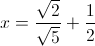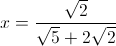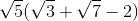We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Factoring Common Factors of Squares and Square Roots

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Factoring And Simplifying Square Roots

Solve for $\dpi{100} x$ :

$x\sqrt{45}+x\sqrt{72}=\sqrt{18}$

Possible Answers:

$x=\frac{\sqrt{2}}{\sqrt{5}}+\frac{1}{2}$

$x=\frac{\sqrt{2}}{\sqrt{5}+2\sqrt{2}}$

$x=\sqrt{9}$

$x=\frac{\sqrt{5}}{\sqrt{2}}+2$

$x=3$

Correct answer:

$x=\frac{\sqrt{2}}{\sqrt{5}+2\sqrt{2}}$

Explanation:

$x\sqrt{45}+x\sqrt{72}=\sqrt{18}$

Notice how all of the quantities in square roots are divisible by 9

$x\sqrt{9\times 5}+x\sqrt{9\times 8}=\sqrt{9\times 2}$

$x\sqrt{9}\sqrt{5}+x\sqrt{9}\sqrt{4\times 2}=\sqrt{9}\sqrt{2}$

$3x\sqrt{5}+3x\sqrt{4}\sqrt{2}=3\sqrt{2}$

$3x\sqrt{5}+6x\sqrt{2}=3\sqrt{2}$

$x(3\sqrt{5}+6\sqrt{2})=3\sqrt{2}$

$x=\frac{3\sqrt{2}}{3\sqrt{5}+6\sqrt{2}}$

Simplifying, this becomes

$x=\frac{\sqrt{2}}{\sqrt{5}+2\sqrt{2}}$

Report an Error

Example Question #1 : How To Find The Common Factor Of Square Roots

Solve for :

$x\sqrt{72}+x\sqrt{108}=12$

Possible Answers:

$x=\frac{3}{\sqrt{2}+\sqrt{3}}$

$x=\frac{3}{\sqrt{5}+\sqrt{3}}$

$x=\frac{2}{\sqrt{6}+\sqrt{7}}$

$x=\frac{2}{\sqrt{2}+\sqrt{3}}$

$x=\frac{2}{\sqrt{3}+\sqrt{6}}$

Correct answer:

$x=\frac{2}{\sqrt{2}+\sqrt{3}}$

Explanation:

$x\sqrt{72}+x\sqrt{108}=12$

Note that all of the square root terms share a common factor of 36, which itself is a square of 6:

$x\sqrt{36\times 2}+x\sqrt{36\times 3}=12$

$6x\sqrt{2}+6x\sqrt{3}=12$

Factoring from both terms on the left side of the equation:

$6x(\sqrt{2}+\sqrt{3})=12$

$6x=\frac{12}{\sqrt{2}+\sqrt{3}}$

$x=\frac{2}{\sqrt{2}+\sqrt{3}}$

Report an Error

Example Question #2 : Basic Squaring / Square Roots

Solve for :

$2x\sqrt{12}+3x\sqrt{28}=18$

Possible Answers:

$x=\frac{9}{2\sqrt{3}+3\sqrt{7}}$

$x=\frac{3}{9\sqrt{2}+3\sqrt{7}}$

$x=\frac{9}{7\sqrt{2}+3\sqrt{5}}$

$x=\frac{3}{2\sqrt{7}+3\sqrt{3}}$

$x=\frac{9}{3\sqrt{2}+7\sqrt{3}}$

Correct answer:

$x=\frac{9}{2\sqrt{3}+3\sqrt{7}}$

Explanation:

$2x\sqrt{12}+3x\sqrt{28}=18$

Note that both $\sqrt{12}$ and $\sqrt{28}$ have a common factor of and is a perfect square:

$2x\sqrt{4\times 3}+3x\sqrt{4\times 7}=18$

$2x\cdot2 \sqrt3 +3x\cdot2\sqrt7=18$

$4x\sqrt{3}+6x\sqrt{7}=18$

From here, we can factor out of both terms on the lefthand side

$2x(2\sqrt{3}+3\sqrt{7})=18$

$x=\frac{18}{2(2\sqrt{3}+3\sqrt{7})}$

$x=\frac{9}{2\sqrt{3}+3\sqrt{7}}$

Report an Error

Example Question #72 : Arithmetic

Solve for :

$x\sqrt{27} + \sqrt{63}=9$

Possible Answers:

$x =\frac{3 -\sqrt{7}}{\sqrt{3}}$

$x =\frac{3 -\sqrt{3}}{\sqrt{7}}$

$x =3\sqrt{7}}$

$x =9\sqrt{3}}$

$x =\frac{3 -\sqrt{7}}{\sqrt{3}}$

Correct answer:

$x =\frac{3 -\sqrt{7}}{\sqrt{3}}$

Explanation:

In order to solve for , first note that all of the square root terms on the left side of the equation have a common factor of 9 and 9 is a perfect square:

$x\sqrt{27} + \sqrt{63}=9$

$x\sqrt{9\times 3} + \sqrt{9\times 7}=9$

$3x\sqrt{3} + 3\sqrt{7}=9$

Simplifying, this becomes:

$3(x\sqrt{3} + \sqrt{7})=9$

$x\sqrt{3} + \sqrt{7}=3$

$x\sqrt{3} =3 -\sqrt{7}$

$x =\frac{3 -\sqrt{7}}{\sqrt{3}}$

Report an Error

Example Question #1 : Basic Squaring / Square Roots

Which of the following is equivalent to:

$\sqrt{210}+\sqrt{55}$ ?

Possible Answers:

$7\sqrt{30}+5\sqrt{11}$

$\sqrt{265}$

$\sqrt{5}(\sqrt{42}+\sqrt{11})$

$5\sqrt{462}$

$5\sqrt{7}+\sqrt{11}$

Correct answer:

$\sqrt{5}(\sqrt{42}+\sqrt{11})$

Explanation:

To begin with, factor out the contents of the radicals. This will make answering much easier:

$\sqrt{210}+\sqrt{55}=\sqrt{2*3*5*7}+\sqrt{5*11}$

They both have a common factor . This means that you could rewrite your equation like this:

$\sqrt{5}\sqrt{2*3*7}+\sqrt{5}\sqrt{11}$

This is the same as:

$\sqrt{5}\sqrt{42}+\sqrt{5}\sqrt{11}$

These have a common $\sqrt{5}$ . Therefore, factor that out:

$\sqrt{5}\sqrt{42}+\sqrt{5}\sqrt{11}=\sqrt{5}(\sqrt{42}+\sqrt{11})$

Report an Error

Example Question #25 : Arithmetic

Simplify:

$\sqrt{15}-\sqrt{20}+\sqrt{35}$

Possible Answers:

$\sqrt{2}(\sqrt{5}+2\sqrt{7})$

$\sqrt{5}(\sqrt{10}-2)$

$\sqrt{7}-3\sqrt{5}$

$2\sqrt{15}+\sqrt{2}$

$\sqrt{5}(\sqrt{3}+\sqrt{7}-2)$

Correct answer:

$\sqrt{5}(\sqrt{3}+\sqrt{7}-2)$

Explanation:

These three roots all have a in common; therefore, you can rewrite them:

$\sqrt{15}-\sqrt{20}+\sqrt{35}=\sqrt{3*5}-\sqrt{4*5}+\sqrt{7*5}$

Now, this could be rewritten:

$\sqrt{3*5}-\sqrt{4*5}+\sqrt{7*5}=\sqrt{5}\sqrt{3}-\sqrt{5}\sqrt{4}+\sqrt{5}\sqrt{7}$

Now, note that $\sqrt{4}=2$

Therefore, you can simplify again:

$\sqrt{5}\sqrt{3}-\sqrt{5}\sqrt{4}+\sqrt{5}\sqrt{7}=\sqrt{5}\sqrt{3}-2\sqrt{5}+\sqrt{5}\sqrt{7}$

Now, that looks messy! Still, if you look carefully, you see that all of your factors have $\sqrt{5}$ ; therefore, factor that out:

$\sqrt{5}\sqrt{3}-2\sqrt{5}+\sqrt{5}\sqrt{7}=\sqrt{5}(\sqrt{3}-2+\sqrt{7})$

This is the same as:

$\sqrt{5}(\sqrt{3}+\sqrt{7}-2)$

Report an Error

Example Question #6 : Basic Squaring / Square Roots

Solve for :

$2x\sqrt{128}-3x\sqrt{192}=16$

Possible Answers:

$\frac{2}{2\sqrt{2}+3\sqrt{3}}$

$\frac{1}{2\sqrt{3}+3\sqrt{2}}$

$\frac{2}{2\sqrt{3}-3\sqrt{2}}$

$\frac{1}{2\sqrt{2}-3\sqrt{3}}$

$\frac{2}{2\sqrt{2}-3\sqrt{3}}$

Correct answer:

$\frac{2}{2\sqrt{2}-3\sqrt{3}}$

Explanation:

Examining the terms underneath the radicals, we find that 128 and 192 have a common factor of . itself is a perfect square, being the product of and . Hence, we recognize that the radicals can be re-written in the following manner:

$\sqrt{128}=\sqrt{64} \sqrt{2}$ , and $\sqrt{192}=\sqrt{64} \sqrt{3}$ .

The equation can then be expressed in terms of these factored radicals as shown:

$2x\sqrt{128}-3x\sqrt{192}=16$

$\Rightarrow 2x(\sqrt64 \sqrt2)-3x(\sqrt{64} \sqrt3)=16$

$\Rightarrow 2x(8)\sqrt2-3x(8)\sqrt3=16$

$\Rightarrow 16x\sqrt2-24x\sqrt3=16$

Factoring the common term from the lefthand side of this equation yields

$8x (2\sqrt2-3x\sqrt3)=16$

Divide both sides by the expression in the parentheses:

$8x=\frac{16}{2\sqrt2-3x\sqrt3}$

Divide both sides by to yield by itself on the lefthand side:

$x=\frac{16}{8(2\sqrt2-3x\sqrt3)}$

Simplify the fraction on the righthand side by dividing the numerator and denominator by :

$x=\frac{2}{2\sqrt{2}-3\sqrt{3}}$

This is the solution for the unknown variable that we have been required to find.

Report an Error

View SAT Mathematics Tutors

Noah
Certified Tutor

Bard College, Bachelors, Philosophy and Creative Writing (Dual Major). Sarah Lawrence College, Master of Fine Arts, Creative ...

View SAT Mathematics Tutors

Priyanka
Certified Tutor

CUNY Hunter College, Bachelor in Arts, Economics.

View SAT Mathematics Tutors

Joy
Certified Tutor

Boston University, Bachelor in Arts, Conservation Biology.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

ISEE Courses & Classes in Philadelphia, SSAT Courses & Classes in Houston, ISEE Courses & Classes in Chicago, ISEE Courses & Classes in Phoenix, LSAT Courses & Classes in Washington DC, GRE Courses & Classes in Denver, SSAT Courses & Classes in Atlanta, SAT Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Houston, GMAT Courses & Classes in Philadelphia

Popular Test Prep

GRE Test Prep in Miami, SSAT Test Prep in Philadelphia, SAT Test Prep in New York City, SSAT Test Prep in Houston, SSAT Test Prep in Denver, GMAT Test Prep in Boston, MCAT Test Prep in Seattle, ACT Test Prep in Denver, LSAT Test Prep in Chicago, ISEE Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Factoring Common Factors of Squares and Square Roots

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #1 : Factoring And Simplifying Square Roots

Example Question #1 : How To Find The Common Factor Of Square Roots

Example Question #2 : Basic Squaring / Square Roots

Example Question #72 : Arithmetic

Example Question #1 : Basic Squaring / Square Roots

Example Question #25 : Arithmetic

Example Question #6 : Basic Squaring / Square Roots

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: