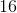SAT Math : How to find the whole from the part
Study concepts, example questions & explanations for SAT Math
All SAT Math Resources
Example Questions
Example Question #1 : Whole And Part
Mr. Owens spent $7.50 for a dinner buffet. The amount he paid accounted for 3/4 of the money in his wallet. How much money is left in his wallet for other expenses?
$1.00
$4.00
$2.50
$10.00
$6.50
$2.50
If $7.50 is 3/4 of the total, 7.50/3 gives us what 1/4 of his total money would be. This equals $2.50, the remaining unspent quarter.
Example Question #1 : How To Find The Whole From The Part
A certain ball that is dropped will bounce back to 3/5 of the height it was initially dropped from. If after the 2nd bounce the ball reaches 39.96 ft, what was the initial height the ball was dropped from?
111 ft
100 ft
135 ft
150 ft
66 ft
111 ft
We know the height of the initial bounce, so work backwards to find the initial height. 39.96/0.6 = 66.6 = height of ball after first bounce
66.6/0.6 = 111 ft
Example Question #1 : How To Find The Whole From The Part
A pitcher of water is filled 
50
30
40
45
35
45
If 
Example Question #81 : Arithmetic
If Mr. Jones’ math class has 8 boys and two-thirds of the class are girls, how many total students are in the class?
If two-thirds of the class are girls, then one-third must be boys. Set up an equation comparing the number of boys to how much they represent in the entire class:
8 = (1/3) x, where x is the number in the entire class.
When we solve for x in the equation we get x = 24.
Example Question #5 : How To Find The Whole From The Part
With the given information, we can set up a proportion.
Certified Tutor
All SAT Math Resources
