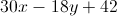Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Middle Level Math : Variables

Study concepts, example questions & explanations for SSAT Middle Level Math

Create An Account

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Variables

Which of the following is NOT the same as

$z\times \frac{(2x+3y)}{3}$

Possible Answers:

$\frac{z}{3}\times(2x+3y)$

$z\times(\frac{2x}{3}+y)$

$\frac{2zx}{3}+zy$

$\frac{2zx +zy}{3}$

$\frac{2zx+3zy}{3}$

Correct answer:

$\frac{2zx +zy}{3}$

Explanation:

The answer shows that the 3 in front of the has been cancelled, but not removed from the denomitator for the .

Report an Error

Example Question #2 : Variables

Simplify: -7 (3x - 11)

Possible Answers:

-21x + 77

-21x+11

-21x-11

21x-77

-21x-77

Correct answer:

-21x + 77

Explanation:

Apply the distributive property:

$-7 (3x - 11) = -7 \cdot 3x - \left (-7 \right ) \cdot 11 = -7 \cdot 3x + 7\cdot 11= -21x + 77$

Report an Error

Example Question #3 : Variables

Simplify: -5 (-3x + 13)

Possible Answers:

15x + 65

-15x - 13

-15x - 65

-15x + 13

15x - 65

Correct answer:

15x - 65

Explanation:

Apply the distributive property:

$-5 (-3x + 13) = -5 (-3x) + \left (-5 \right ) \cdot 13= 5\cdot 3x - 5\cdot 13 = 15x -65$

Report an Error

Example Question #2 : Operations

Simplify: $-6 \left ( 5x - 3y - 9 \right )$

Possible Answers:

-30x - 3y - 9

-30x - 18y + 54

-30x + 18y - 54

-30x + 3y + 9

-30x + 18y + 54

Correct answer:

-30x + 18y + 54

Explanation:

Apply the distributive property:

$-6 \left ( 5x - 3y - 9 \right )= -6 \cdot 5x - \left (-6 \right ) \cdot 3y - \left (-6 \right ) \cdot 9$

$= -6 \cdot 5x + 6 \cdot 3y + 6 \cdot 9$

= -30x + 18y + 54

Report an Error

Example Question #4 : Variables

Simplify: $6 \left ( 5x - 3y + 7 \right )$

Possible Answers:

30x - 18y + 7

30x - 18y - 42

30x - 18y + 42

30x - 18y - 7

30x - 6y + 7

Correct answer:

30x - 18y + 42

Explanation:

Apply the distributive property:

$6 \left ( 5x - 3y + 7 \right ) = 6 \cdot 5x - 6 \cdot 3y + 6 \cdot 7=30x - 18y + 42$

Report an Error

Example Question #3 : Operations

Shaun has twice as much money as Jessica. Jessica has one third as much money as Chris. Shaun has half as much money as Carmen. Who has the most money?

Possible Answers:

Shaun

Chris

Jessica

Carmen

Both Shaun and Carmen

Correct answer:

Carmen

Explanation:

In order to figure out who has the most money, we must organize the data we have. Since Shaun has more money than Jessica, let us use Jessica as our baseline. So, if the money that Jessica has is represented by , the money Shaun has will be because he has twice as much money as Jessica.

Jessica =

Shaun =

Next, we know that Jessica has one third as much money as Chris. In other words, Chris has three times as much money as Jessica. This can be represented by . We then learn that Shaun has half as much money as Carmen or, in other words, Carmen has two times the amount of money Shaun has. Since Shaun has dollars, that must mean Carmen has dollars because $2\times 2m = 4m$ . So, by comparing everyone side-by-side, we can see that Carmen has the most money as she has four times the amount of money that Jessica has.

Jessica =

Shaun =

Chris =

Carmen =

Carmen is the answer.

Report an Error

Example Question #4 : Operations

Given x = 3 , y=6 , and z=3 , compute xyz .

Possible Answers:

Correct answer:

Explanation:

xyz refers to the product of the three variables: $3\cdot 6\cdot 3=54$ .

Report an Error

Example Question #1 : Multiplying And Dividing Polynomials

Simplify:

$4m\cdot3m$

Possible Answers:

$12m^{3}$

$12m^{2}$

12m

24m

$6m^{2}$

Correct answer:

$12m^{2}$

Explanation:

To solve, you can use the commutative and associative properties of multiplication to group like-terms together.

$4m\cdot3m=4\times m\times 3\times m=4\times3\times m\times m$

The 4 and 3 should be first multiplied, resulting in 12.

$12\times m\times m$

Next should be multiplied by , giving us $m^{2}$ .

$12\times m^2$

12 times $m^{2}$ is equal to $12m^{2}$ .

Therefore, the correct answer is $12m^{2}$ .

Report an Error

Example Question #3 : How To Multiply Variables

Simplify:

3a(2a+4)-7

Possible Answers:

$6a^{2}+12a$

$a^{2}+12a-7$

6a+12a-7

$6a^{2}+12-7a$

$6a^{2}+12a-7$

Correct answer:

$6a^{2}+12a-7$

Explanation:

When simplifying this expression, the first step is to apply the distributive property.

3a(2a+4)-7

$(3a\times2a)+(3a\times4)-7$

$6a^{2}+12a-7$

Next, we assert whether the expression can be reduced further. It cannot, as there are no like-terms to combine.

Therefore, the correct answer is $6a^{2}+12a-7$ .

Report an Error

Example Question #1 : Operations

Suppose you know the values of all variables in the expression

$x \cdot\left ( y + b \right )^{2}$

and you want to evaluate the expression.

In which order will you carry out the operations?

Possible Answers:

Adding, multiplying, squaring

Squaring, multiplying, adding

Multiplying, squaring, adding

Multiplying, adding, squaring

Adding, squaring, multiplying

Correct answer:

Adding, squaring, multiplying

Explanation:

By the order of operations, the operation inside grouping symbols, which here is addition, takes precendence, followed by, in order, squaring and multiplication.

Report an Error

View SSAT- Middle Level Tutors

Gabby
Certified Tutor

University of Oregon, Bachelor in Arts, Journalism. University of Oregon, Current Grad Student, Communication, General.

View SSAT- Middle Level Tutors

Aneeb
Certified Tutor

CUNY Lehman College, Bachelor in Arts, Arts, General.

View SSAT- Middle Level Tutors

Aileen
Certified Tutor

Zhongshan University University of Hawaii-Manoa, Bachelor in Arts, Foreign Languages and Literatures, General. Universite de ...

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

French Tutors in Boston, Computer Science Tutors in Atlanta, Statistics Tutors in Chicago, Statistics Tutors in Houston, MCAT Tutors in Atlanta, Physics Tutors in Philadelphia, Calculus Tutors in Chicago, SSAT Tutors in Houston, Chemistry Tutors in Dallas Fort Worth, Biology Tutors in Boston

Popular Courses & Classes

SSAT Courses & Classes in Houston, GMAT Courses & Classes in Houston, LSAT Courses & Classes in New York City, ACT Courses & Classes in New York City, LSAT Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in Miami, LSAT Courses & Classes in Philadelphia, Spanish Courses & Classes in Miami, GRE Courses & Classes in Boston

Popular Test Prep

GMAT Test Prep in Washington DC, ISEE Test Prep in Boston, LSAT Test Prep in Chicago, ACT Test Prep in San Francisco-Bay Area, SAT Test Prep in Chicago, SAT Test Prep in Dallas Fort Worth, ISEE Test Prep in Philadelphia, MCAT Test Prep in Washington DC, ACT Test Prep in Seattle, LSAT Test Prep in Los Angeles

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Middle Level Math : Variables

Study concepts, example questions & explanations for SSAT Middle Level Math

All SSAT Middle Level Math Resources

Example Questions

Example Question #1 : Variables

Example Question #2 : Variables

Example Question #3 : Variables

Example Question #2 : Operations

Example Question #4 : Variables

Example Question #3 : Operations

Example Question #4 : Operations

Example Question #1 : Multiplying And Dividing Polynomials

Example Question #3 : How To Multiply Variables

Example Question #1 : Operations

All SSAT Middle Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: