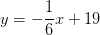Lines that are parallel must have the same slope. Thus, the correct answer must also have a slope of \(\displaystyle 9\).

First, put the equation in the more familiar \(\displaystyle y=mx+b\) format to see what the slope of the given line is.

\(\displaystyle 2x-y=4\)

\(\displaystyle y=2x-4\)

Lines that are parallel must have the same slope. Thus, the correct answer must also have a slope of \(\displaystyle 2\).

First, put the given equation in the more familiar \(\displaystyle y=mx+b\) format to find out the slope of the given line.

\(\displaystyle -4x+\frac{1}{2}y=8\)

\(\displaystyle \frac{1}{2}y=4x+8\)

\(\displaystyle y=8x+16\)

 Lines that are parallel must share the same slope. Thus, the line that is parallel has a slope of \(\displaystyle 8\).

Lines that are parallel have the same slope, so the correct answer must also have the slope of \(\displaystyle 6\).

For two lines to be parallel, their slopes must be the same. Thus, the line that is parallel to the given one must also have a slope of \(\displaystyle -4\).

These two lines must share the same slope of \(\displaystyle -3\) to be parallel. You can identify the slope of a line in \(\displaystyle y=mx+b\) form easily, as the slope is the value of \(\displaystyle m\). The only answer choice that has a slope of \(\displaystyle -3\) is \(\displaystyle y=-3x-1\), so it is the correct answer.

First write the equation in slope intercept form. Add \(\displaystyle 12x\) to both sides to get \(\displaystyle 4y = 12x + 2\). Now divide both sides by \(\displaystyle 4\) to get \(\displaystyle y = 3x + 0.5\). The slope of this line is \(\displaystyle 3\), so any line that also has a slope of \(\displaystyle 3\) would be parallel to it. The correct answer is  \(\displaystyle x - \frac{1}{3}y = 7\).

Parallel lines will always have equal slopes. The slope can be found quickly by observing the equation in slope-intercept form and seeing which number falls in the "\(\displaystyle m\)" spot in the linear equation \(\displaystyle (y=mx+b)\), 

We are looking for an answer choice in which both equations have the same \(\displaystyle m\) value. Both lines in the correct answer have a slope of 2, therefore they are parallel.

Lines are parallel when their slopes are the same.

First, we need to place the given equation in the slope-intercept form.

\(\displaystyle -4y=-10+26\)

\(\displaystyle y=\frac{10}{4}x-\frac{26}{4}\)

\(\displaystyle y=\frac{5}{2}x-\frac{13}{2}\)

Because the given line has the slope of \(\displaystyle \frac{5}{2}\), the line parallel to it must also have the same slope.

Parallel lines have the same slope. The slope of a line in slope-intercept form \(\displaystyle (y=mx+b)\) is the value of \(\displaystyle m\). So, the slope of the line \(\displaystyle y=-\frac{1}{5}x+1\) is \(\displaystyle -\frac{1}{5}\). That means that for the two lines to be parallel, the slope of the second line must also be \(\displaystyle -\frac{1}{5}\).