Call Now to Set Up Tutoring:

(888) 888-0446

7th Grade Math : Geometry

Study concepts, example questions & explanations for 7th Grade Math

Create An Account

All 7th Grade Math Resources

8 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Geometry

If a rectangle possesses a width of $2\textup{ inches}$ and has a perimeter of $18\textup{ inches}$ , then what is the length?

Possible Answers:

$16\textup{ inches}$

$8\textup{ inches}$

$7\textup{ inches}$

$14\textup{ inches}$

Correct answer:

$7\textup{ inches}$

Explanation:

In order to solve this problem, we need to recall the formula for perimeter of a rectangle:

P=2l+2w

We can substitute in our known values and solve for our unknown variable (i.e. length):

18=2l+2(2)

18=2l+4

We want to isolate the to one side of the equation. In order to do this, we will first subtract from both sides of the equation.

$\frac{\begin{array}[b]{r}18=2l+4\\ -4\ \ \ \ \ \ -4\end{array}}{\\\\14=2l}$

Next, we can divide each side by

$\frac{\begin{array}[b]{r}\frac{14}{2}=\frac{2l}{2}\\\end{array}}{7=l}$

The length of the rectangle is $7\textup{ inches}$

Report an Error

Example Question #1 : Geometry

The figure represents a set of supplementary angles, solve for .

Possible Answers:

$82^\circ$

$83^\circ$

$84^\circ$

$81^\circ$

Correct answer:

$81^\circ$

Explanation:

Supplementary angles are defined as two angles that when added together equal $180^\circ$

From the question, we know that the two angles are supplementary, and thus equal $180^\circ$ , so we can set up the following equation:

x+99=180

Next we can solve for :

$\frac{\begin{array}[b]{r}x+99=180\\ -99\ \ -99\end{array}}{x= 81}$

Report an Error

Example Question #2 : Geometry

What is the area of the circle provided?

Possible Answers:

$40\pi\textup{ in}^2$

$1\textup,400\pi\textup{ in}^2$

$1\textup,600\pi\textup{ in}^2$

$400\pi\textup{ in}^2$

Correct answer:

$400\pi\textup{ in}^2$

Explanation:

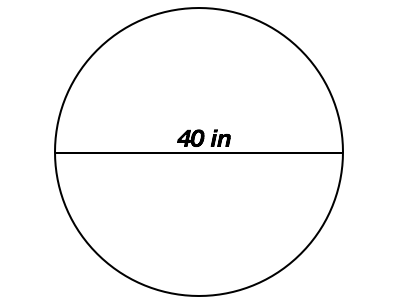
In order to solve this problem, we need to recall the formula for the area of a circle:

$A= r^2\pi$

The circle in this question provides us with the diameter, so we first have to solve for the radius. Remember, the radius is half the diameter:

$r=\frac{d}{2}$

$r=\frac{40}{2}$

r=20

Now that we have the radius we can use the formula to solve:

$A=20^2\pi$

Solve:

$A=400\pi\textup{ in}^2$

Report an Error

Example Question #2 : Geometry

6 8 10

What is the area of the triangle pictured above?

Possible Answers:

Correct answer:

Explanation:

The area of a triangle is calculated using the formula $Area = \frac{1}{2}(Base\times Height)$ . Importantly, the height is a perpendicular line between the base and the opposite point. In a right triangle like this one, you're in luck: the triangle as drawn already has that perpendicular line as one of the two sides. So here we will calculate $\frac{1}{2}(8\times 6)$ . That gives us an answer of 24.

Report an Error

View Tutors

Richard
Certified Tutor

CUNY Brooklyn College, Bachelor of Science, Chemistry. CUNY Brooklyn College, Master of Arts, Experimental Psychology.

View Tutors

Joy
Certified Tutor

Boston University, Bachelor in Arts, Conservation Biology.

View Tutors

Sarah
Certified Tutor

New York University, Bachelor of Fine Arts, Drama.

All 7th Grade Math Resources

8 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Washington DC, GMAT Tutors in Denver, SAT Tutors in Los Angeles, ACT Tutors in Miami, Calculus Tutors in Seattle, Spanish Tutors in Dallas Fort Worth, Calculus Tutors in San Francisco-Bay Area, Spanish Tutors in Phoenix, Calculus Tutors in Boston, ACT Tutors in Dallas Fort Worth

Popular Courses & Classes

ACT Courses & Classes in Denver, SAT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in Phoenix, Spanish Courses & Classes in New York City, MCAT Courses & Classes in Seattle, LSAT Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Philadelphia, GMAT Courses & Classes in Philadelphia, MCAT Courses & Classes in Dallas Fort Worth

Popular Test Prep

ISEE Test Prep in Phoenix, GMAT Test Prep in Philadelphia, ACT Test Prep in Los Angeles, ACT Test Prep in Denver, ACT Test Prep in San Francisco-Bay Area, SSAT Test Prep in Philadelphia, MCAT Test Prep in Seattle, MCAT Test Prep in San Francisco-Bay Area, MCAT Test Prep in Dallas Fort Worth, MCAT Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

7th Grade Math : Geometry

Study concepts, example questions & explanations for 7th Grade Math

All 7th Grade Math Resources

Example Questions

Example Question #1 : Geometry

Example Question #1 : Geometry

Example Question #2 : Geometry

Example Question #2 : Geometry

All 7th Grade Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: