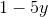Call Now to Set Up Tutoring:

(888) 888-0446

ACT Math : Algebraic Fractions

Study concepts, example questions & explanations for ACT Math

Create An Account

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #3 : Mixed / Improper Fractions

$\frac{34}{5}$

Change to a mixed number

Possible Answers:

$3\frac{4}{5}$

$4 \frac{6}{5}$

$6\frac{4}{5}$

$4 \frac{5}{6}$

$34\frac{1}{5}$

Correct answer:

$6\frac{4}{5}$

Explanation:

To convert from a fraction to a mixed number we must find out how many times the denominator goes into the numerator using division and the remainder becomes the new fraction.

$\frac{34}{5} = 6\ r 4 \ so \6\frac{4}{5}$

Report an Error

Example Question #1 : Algebraic Fractions

What is the average of $\frac{2}{3}$ and $\frac{5}{6}$ ?

Possible Answers:

$\frac{4}{5}$

$\frac{6}{7}$

$\frac{11}{12}$

$\frac{3}{4}$

Correct answer:

$\frac{3}{4}$

Explanation:

To average, we have to add the values and divide by two. To do this we need to find a common denomenator of 6. We then add and divide by 2, yielding 4.5/6. This reduces to 3/4.

Report an Error

Example Question #2 : Algebraic Fractions

Which of the following is equivalent to $\frac{x}{2}+\frac{x-5}{x+3}$ ?

Possible Answers:

$\frac{x^{2}+5x-10}{2x+6}$

None of the answers are correct

$\frac{x^{2}-5x+10}{2x+6}$

$\frac{2x-5}{x+5}$

$\frac{x^{2}-5x}{2x+6}$

Correct answer:

$\frac{x^{2}+5x-10}{2x+6}$

Explanation:

This problem is solved the same way ½ + 1/3 is solved. For example, ½ + 1/3 = 3/6 + 2/6 = 5/6. Find a common denominator then convert each fraction into an equivalent fraction using that common denominator. The final step is to add the two new fractions and simplify.

Report an Error

Example Question #3 : Algebraic Fractions

A train travels at a constant rate of meters per second. How many kilometers does it travel in minutes? $(1\ km=1000\ m)$

Possible Answers:

Correct answer:

Explanation:

Set up the conversions as fractions and solve:

$\dpi{100} \small \frac{20m}{1sec}\times \frac{60sec^}{1min}\times \frac{1km}{1000m}\times \frac{10min}{1}$

Report an Error

Example Question #4 : Algebraic Fractions

Simplify. $\frac{4x^{4}z^{3}}{2xz^{2}}$

Possible Answers:

$2x^{3}z$

$4x^{3}z$

Can't be simplified

$2x^{4}z^{3}$

$\frac{2x^{4}z^{3}}{xz}$

Correct answer:

$2x^{3}z$

Explanation:

To simplify exponents which are being divided, subtract the exponents on the bottom from exponents on the top. Remember that only exponents with the same bases can be simplified

Report an Error

Example Question #5 : Algebraic Fractions

Simplify:

$\frac{x^2-y^2}{x+y}$

Possible Answers:

$x-y,\ x+y$

x+y

2xy

x-y

Correct answer:

x-y

Explanation:

x² – y² can be also expressed as (x + y)(x – y).

Therefore, the fraction now can be re-written as (x + y)(x – y)/(x + y).

This simplifies to (x – y).

Report an Error

Example Question #6 : Algebraic Fractions

Simplify:

$\frac{x\sqrt{2}-2\sqrt{2}}{\sqrt{2x}+2}$

Possible Answers:

$\sqrt{x}-\sqrt{2}$

$\frac{x+2}{\sqrt{x-2}}$

$x+\sqrt{2}$

$\sqrt{x}+\sqrt{2}$

$x-\sqrt{2}$

Correct answer:

$\sqrt{x}-\sqrt{2}$

Explanation:

Notice that the $\sqrt{2}$ term appears frequently. Let's try to factor that out:

$\frac{x\sqrt{2}-2\sqrt{2}}{\sqrt{2x}+2} = \frac{\sqrt{2}*(x-2)}{\sqrt{2}*(\sqrt{x} +\sqrt{2})} = \frac{x-2}{\sqrt{x} +\sqrt{2}}$

Now multiply both the numerator and denominator by the conjugate of the denominator:

$\frac{x-2}{\sqrt{x} +\sqrt{2}} * \frac{\sqrt{x} -\sqrt{2}}{\sqrt{x} -\sqrt{2}} =\frac{(x-2)*(\sqrt{x} -\sqrt{2})}{x-2} =\sqrt{x} -\sqrt{2}$

Report an Error

Example Question #7 : Algebraic Fractions

Simplify:

(2x + 4)/(x + 2)

Possible Answers:

x + 2

2x + 2

x + 1

x + 4

Correct answer:

Explanation:

(2x + 4)/(x + 2)

To simplify you must first factor the top polynomial to 2(x + 2). You may then eliminate the identical (x + 2) from the top and bottom leaving 2.

Report an Error

Example Question #8 : Algebraic Fractions

Simplify the following expression:

$\frac{2x^{4}-32}{2x^{2}-8}$

Possible Answers:

$x^{2}-4$

$2$

$2(x^{2}-4)$

$(x+2)(x-2)$

$x^{2}+4$

Correct answer:

$x^{2}+4$

Explanation:

Factor both the numerator and the denominator:

$\frac{2(x^{2}-4)(x^{2}+4)}{2(x^{2}-4)}$

After reducing the fraction, all that remains is:

$(x^{2}+4)$

Report an Error

Example Question #9 : Algebraic Fractions

Simplify:

$\frac{x^{2}y-5x^{2}y^{2}}{x^{2}y}$

Possible Answers:

1-5y

$5+x^{2}y^{2}$

y-5y

1-5x

None of the other answers

Correct answer:

1-5y

Explanation:

With this problem the first thing to do is cancel out variables. The x²can all be divided by each other because they are present in each system. The equation will now look like this:

$\frac{y-5y^{2}}{y}$

Now we can see that the equation can all be divided by y, leaving the answer to be:

1-5y

Report an Error

View ACT Math Tutors

Anne
Certified Tutor

University of Maryland-Baltimore, Doctor of Science, Accounting.

View ACT Math Tutors

Satweka
Certified Tutor

The University of Texas at Dallas, Master of Science, Biomedical Engineering.

View ACT Math Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

ACT Math Tutors in Top Cities:

Atlanta ACT Math Tutors, Austin ACT Math Tutors, Boston ACT Math Tutors, Chicago ACT Math Tutors, Dallas Fort Worth ACT Math Tutors, Denver ACT Math Tutors, Houston ACT Math Tutors, Kansas City ACT Math Tutors, Los Angeles ACT Math Tutors, Miami ACT Math Tutors, New York City ACT Math Tutors, Philadelphia ACT Math Tutors, Phoenix ACT Math Tutors, San Diego ACT Math Tutors, San Francisco-Bay Area ACT Math Tutors, Seattle ACT Math Tutors, St. Louis ACT Math Tutors, Tucson ACT Math Tutors, Washington DC ACT Math Tutors

Popular Courses & Classes

GMAT Courses & Classes in Los Angeles, SAT Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Atlanta, Spanish Courses & Classes in San Diego, MCAT Courses & Classes in Boston, MCAT Courses & Classes in Seattle, GRE Courses & Classes in Denver, SAT Courses & Classes in Boston, GMAT Courses & Classes in Denver, Spanish Courses & Classes in Dallas Fort Worth

Popular Test Prep

MCAT Test Prep in Denver, GMAT Test Prep in Denver, ISEE Test Prep in Philadelphia, GMAT Test Prep in Miami, SAT Test Prep in Dallas Fort Worth, SAT Test Prep in Miami, ISEE Test Prep in Dallas Fort Worth, ISEE Test Prep in Boston, GMAT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ACT Math : Algebraic Fractions

Study concepts, example questions & explanations for ACT Math

All ACT Math Resources

Example Questions

Example Question #3 : Mixed / Improper Fractions

Example Question #1 : Algebraic Fractions

Example Question #2 : Algebraic Fractions

Example Question #3 : Algebraic Fractions

Example Question #4 : Algebraic Fractions

Example Question #5 : Algebraic Fractions

Example Question #6 : Algebraic Fractions

Example Question #7 : Algebraic Fractions

Example Question #8 : Algebraic Fractions

Example Question #9 : Algebraic Fractions

All ACT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: