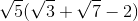To solve the equation \(\displaystyle \sqrt{2016} + \sqrt{896} = ?\), we can first factor the numbers under the square roots.

\(\displaystyle \sqrt{2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 3\cdot 3\cdot 7} + \sqrt{2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 7} = ?\)

When a factor appears twice, we can take it out of the square root.

\(\displaystyle 2\cdot 2\cdot 3\sqrt{2\cdot 7} + 2\cdot 2\cdot 2\sqrt{2\cdot 7} = ?\)

\(\displaystyle 12\sqrt{14} + 8 \sqrt{14} = ?\)

Now the numbers can be added directly because the expressions under the square roots match.

\(\displaystyle 12\sqrt{14} + 8\sqrt{14} = 20\sqrt{14}\)

First, we can simplify the radicals by factoring.

\(\displaystyle x\sqrt{96} + x\sqrt{150} = \sqrt{162}\)

\(\displaystyle x\sqrt{2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 3} + x\sqrt{2\cdot 3\cdot 5\cdot 5} = \sqrt{2\cdot 3\cdot 3\cdot 3\cdot 3}\)

\(\displaystyle x\left (2\cdot 2 \right )\sqrt{2\cdot 3} + x\left ( 5\right )\sqrt{2\cdot 3} = \left (3\cdot 3 \right )\sqrt{2}\)

\(\displaystyle 4x\sqrt{6} + 5x\sqrt{6} = 9\sqrt{2}\)

Now, we can factor out the \(\displaystyle x\).

\(\displaystyle x\left (4\sqrt{6} + 5\sqrt{6} \right ) = 9\sqrt{2}\)

\(\displaystyle x\left (9\sqrt{6} \right ) = 9\sqrt{2}\)

Now divide and simplify.

\(\displaystyle x = \frac{9\sqrt{2}}{9\sqrt{6} } = \frac{\sqrt{2}}{\sqrt{2\cdot 3}} = \frac{1}{\sqrt{3}}\)

To begin with, factor out the contents of the radicals.  This will make answering much easier:

\(\displaystyle \sqrt{210}+\sqrt{55}=\sqrt{2*3*5*7}+\sqrt{5*11}\)

They both have a common factor \(\displaystyle 5\).  This means that you could rewrite your equation like this:

\(\displaystyle \sqrt{5}\sqrt{2*3*7}+\sqrt{5}\sqrt{11}\)

This is the same as:

\(\displaystyle \sqrt{5}\sqrt{42}+\sqrt{5}\sqrt{11}\)

These have a common \(\displaystyle \sqrt{5}\).  Therefore, factor that out:

\(\displaystyle \sqrt{5}\sqrt{42}+\sqrt{5}\sqrt{11}=\sqrt{5}(\sqrt{42}+\sqrt{11})\)

These three roots all have a \(\displaystyle 5\) in common; therefore, you can rewrite them:

\(\displaystyle \sqrt{15}-\sqrt{20}+\sqrt{35}=\sqrt{3*5}-\sqrt{4*5}+\sqrt{7*5}\)

Now, this could be rewritten:

\(\displaystyle \sqrt{3*5}-\sqrt{4*5}+\sqrt{7*5}=\sqrt{5}\sqrt{3}-\sqrt{5}\sqrt{4}+\sqrt{5}\sqrt{7}\)

Now, note that \(\displaystyle \sqrt{4}=2\)

Therefore, you can simplify again:

\(\displaystyle \sqrt{5}\sqrt{3}-\sqrt{5}\sqrt{4}+\sqrt{5}\sqrt{7}=\sqrt{5}\sqrt{3}-2\sqrt{5}+\sqrt{5}\sqrt{7}\)

Now, that looks messy! Still, if you look carefully, you see that all of your factors have \(\displaystyle \sqrt{5}\); therefore, factor that out:

\(\displaystyle \sqrt{5}\sqrt{3}-2\sqrt{5}+\sqrt{5}\sqrt{7}=\sqrt{5}(\sqrt{3}-2+\sqrt{7})\)

This is the same as:

\(\displaystyle \sqrt{5}(\sqrt{3}+\sqrt{7}-2)\)

Begin by factoring out the relevant squared data:

\(\displaystyle x\sqrt{50}+x\sqrt{8}-\sqrt{18}+\sqrt{98}\) is the same as

\(\displaystyle x\sqrt{25*2}+x\sqrt{4*2}-\sqrt{9*2}+\sqrt{49*2}\)

This can be simplified to:

\(\displaystyle 5x\sqrt{2}+2x\sqrt{2}-3\sqrt{2}+7\sqrt{2}\)

Since your various factors contain square roots of \(\displaystyle 2\), you can simplify:

\(\displaystyle 7x\sqrt{2}+4\sqrt{2}\)

Technically, you can factor out a \(\displaystyle \sqrt{2}\):

\(\displaystyle \sqrt{2}(7x+4)\)

Begin by breaking apart the square roots on the left side of the equation:

\(\displaystyle t\sqrt{4*7}-t\sqrt{9*7}=\sqrt{14}\)

This can be rewritten:

\(\displaystyle 2t\sqrt{7}-3t\sqrt{7}=\sqrt{14}\)

You can combine like terms on the left side:

\(\displaystyle -t\sqrt{7}=\sqrt{14}\)

Solve by dividing both sides by \(\displaystyle -\sqrt{7}\):

\(\displaystyle t=\frac{-\sqrt{14}}{\sqrt{7}}\)

This simplifies to:

\(\displaystyle t=-\sqrt{2}\)

To begin solving this problem, find the greatest common perfect square for all quantities under a radical.

\(\displaystyle x\sqrt{28} + x\sqrt{84} = 12\) ---> \(\displaystyle x\sqrt{4 \cdot 7} + x\sqrt{4 \cdot 21} = 12\)

Pull \(\displaystyle 4\) out of each term on the left:

\(\displaystyle x\sqrt{4 \cdot 7} + x\sqrt{4 \cdot 21} = 12\) ---> \(\displaystyle 2x\sqrt{7} + 2x\sqrt{21} = 12\)

Next, factor out \(\displaystyle 2x\) from the left-hand side:

\(\displaystyle 2x\sqrt{7} + 2x\sqrt{21} = 12\) ---> \(\displaystyle 2x(\sqrt{7} +\sqrt{21}) = 12\)

Lastly, isolate \(\displaystyle x\):

\(\displaystyle 2x(\sqrt{7} +\sqrt{21}) = 12\) ---> \(\displaystyle x = \frac{6}{(\sqrt{7} +\sqrt{21})}\)

Solving this one is tricky. At first glance, we have no common perfect square to work with. But since each term can produce the quantity \(\displaystyle \sqrt{5}\), let's start there:

\(\displaystyle x\sqrt{125} + 5x\sqrt{70} = \sqrt{5}\) ---> \(\displaystyle x\sqrt{25 \cdot 5} + 5x\sqrt{12 \cdot 5} = \sqrt{5}\)

Simplify the first term:

\(\displaystyle x\sqrt{25 \cdot 5} + 5x\sqrt{12 \cdot 5} = \sqrt{5}\) ---> \(\displaystyle 5x\sqrt{5} + 5x\sqrt{12 \cdot 5} = \sqrt{5}\)

Divide all terms by \(\displaystyle \sqrt{5}\) to simplify, 

\(\displaystyle 5x\sqrt{5} + 5x\sqrt{12 \cdot 5} = \sqrt{5}\) ---> \(\displaystyle 5x + 5x\sqrt{12} = 1\)

Next, factor out \(\displaystyle 5x\) from the left-hand side:

\(\displaystyle 5x + 5x\sqrt{12} = 1\) ---> \(\displaystyle 5x(1+ \sqrt{12}) = 1\)

Isolate \(\displaystyle x\) by dividing by \(\displaystyle 5(1+\sqrt{12})\) and simplifying:

\(\displaystyle 5x(1+ \sqrt{12}) = 1\) ---> \(\displaystyle x = \frac{1}{5+5\sqrt{12}}\)

Last, simplify the denominator:

\(\displaystyle x = \frac{1}{5+5\sqrt{12}}\) ----> \(\displaystyle x = \frac{1}{5+10\sqrt{3}}\)

Right away, we notice that \(\displaystyle \sqrt{23}\) is a prime radical, so no simplification is possible. Note, however, that both other radicals are divisible by \(\displaystyle \sqrt{23}\).

Our first step then becomes simplifying the equation by dividing everything by \(\displaystyle \sqrt{23}\):

\(\displaystyle x\sqrt{23} - x\sqrt{69} = 12\sqrt{115}\) ---> \(\displaystyle x-x\sqrt{3} = 12\sqrt{5}\)

Next, factor out \(\displaystyle x\) from the left-hand side:

\(\displaystyle x-x\sqrt{3} = 12\sqrt{5}\) ---> \(\displaystyle x(1-\sqrt{3}) = 12\sqrt{5}\)

Lastly, isolate \(\displaystyle x\):

\(\displaystyle x(1-\sqrt{3}) = 12\sqrt{5}\) ---> \(\displaystyle x = \frac{12\sqrt{5}}{1-\sqrt{3}}\)

Once again, there are no common perfect squares under the radical, but with some simplification, the equation can still be solved for \(\displaystyle x\):

\(\displaystyle -4x\sqrt{\frac{1}{4}} + \frac{2}{3}x\sqrt{27} = \sqrt{15}\) ---> \(\displaystyle (\frac{1}{2}\cdot -4x) + (3 \cdot\frac{2}{3}x\sqrt{3}) = \sqrt{15}\)

Simplify:

\(\displaystyle (\frac{1}{2}\cdot -4x) + (3 \cdot\frac{2}{3}x\sqrt{3}) = \sqrt{15}\) ---> \(\displaystyle (-2x) + (2x\sqrt{3}) = \sqrt{15}\)

Factor out \(\displaystyle 2x\) from the left-hand side:

\(\displaystyle (-2x) + (2x\sqrt{3}) = \sqrt{15}\) ---> \(\displaystyle 2x(-1 + \sqrt{3}) = \sqrt{15}\)

Lastly, isolate \(\displaystyle x\):

\(\displaystyle 2x(-1 + \sqrt{3}) = \sqrt{15}\) ---> \(\displaystyle x= \frac{\sqrt{15}}{-2+2\sqrt{3}}\)