To find the length of the diagonal, we need to use the Pythagorean Theorem. Therefore, we need to sketch the following triangle within trapezoid $\displaystyle ABCD$:

We know that the base of the triangle has length $\displaystyle 9\: m$. By subtracting the top of the trapezoid from the bottom of the trapezoid, we get:

$\displaystyle 12\: m - 6\: m = 6\: m$

Dividing by two, we have the length of each additional side on the bottom of the trapezoid:

$\displaystyle \frac{6\: m}{2} = 3\: m$

Adding these two values together, we get $\displaystyle 9\: m$.

The formula for the length of diagonal $\displaystyle AC$ uses the Pythagoreon Theorem:

$\displaystyle AC^2 = AE^2 + EC^2$, where $\displaystyle E$ is the point between $\displaystyle A$ and $\displaystyle D$ representing the base of the triangle.

Plugging in our values, we get:

$\displaystyle AC^2 = (9\: m)^2 + (4\: m)^2$

$\displaystyle AC^2 = 81\: m^2 + 16\: m^2$

$\displaystyle AC^2 = 97\: m^2$

$\displaystyle AC = \sqrt{97}\: m$

All of the lengths with one mark have length 5, and all of the side lengths with two marks have length 4. With this knowledge, we can add side lengths together to find that one diagonal is the hypotenuse to this right triangle:

Using Pythagorean Theorem gives:

$\displaystyle 4^2 + 9^2 = C^2$

$\displaystyle 16+81=C^2$

$\displaystyle 97 = C^2$ take the square root of each side

$\displaystyle \sqrt{97}= C$

Similarly, the other diagonal can be found with this right triangle:

Once again using Pythagorean Theorem gives an answer of $\displaystyle \sqrt{65}$

To find the length of the diagonals, split the top side into 3 sections as shown below:

The two congruent sections plus 8 adds to 14. $\displaystyle 14 - 8 = 6$, so the two congruent sections add to 6. They must each be 3. This means that the top of the right triangle with the diagonal as a hypotenuse must be 11, since $\displaystyle 14-3=11$.

We can solve for the diagonal, now pictured, using Pythagorean Theorem:

$\displaystyle 11^2 + 8^2 = C^2$

$\displaystyle 121 + 64 = C^2$

$\displaystyle 185 = C^2$ take the square root of both sides

$\displaystyle \sqrt{185}=C$

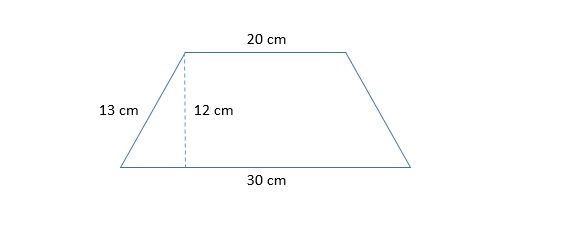
In order to calculate the length of the diagonal, we first must assume that the height is perpendicular to both the top and bottom of the trapezoid. 

Knowing this, we can draw in the diagonal as shown below and use the Pythagorean Theorem to solve for the diagonal. 

$\displaystyle Using\ the\ pythagorean\ theorem\ we\ get: 12^2+20^2=diagonal^2$

$\displaystyle This\ simplifies\ to\ become\ 144+400=diagonal^2$

$\displaystyle 544=diagonal^2$

We now take the square root of both sides: 

$\displaystyle \sqrt544=\sqrt diagonal^2$

$\displaystyle \sqrt16*\sqrt34=diagonal$

$\displaystyle 4\sqrt34=diagonal$

1) The diagonal $\displaystyle \overline{AB}$ can be found from $\displaystyle \bigtriangleup BAE$ by using the Pythagorean Theorem.

2) The length of the base of $\displaystyle \bigtriangleup CAD$, $\displaystyle \overline{AD}$ has to be found because $\displaystyle AE = AD + DE$ is the length of the base of $\displaystyle \bigtriangleup BAE$.

3) $\displaystyle AE = 5 + AD$.

4) Using the Pythagorean Theorem on $\displaystyle \bigtriangleup CAD$ to find $\displaystyle m(\overline{AD})$,

$\displaystyle 4^{2} = 3^{2} + (AD)^{2}$

$\displaystyle 4^{2} - 3^{2} = (AD)^{2}$

$\displaystyle 16 - 9 = (AD)^{2}$

$\displaystyle 7 = (AD)^{2}$

$\displaystyle \sqrt{7} = AD$

5) Using the Pythagorean Theorem on $\displaystyle \bigtriangleup BAE$ to find $\displaystyle m(\overline{AB})$,

$\displaystyle (AB)^{2} = (5 + \sqrt{7})^{2} + 3^{2}$

$\displaystyle = 5^{2} + 2(5\cdot \sqrt{7}) + (\sqrt{7})^{2} + 9$

$\displaystyle = 25 + 10\cdot \sqrt{7} + 7 + 9$

$\displaystyle = 41 + 10\sqrt{7}$

$\displaystyle \sqrt{(AB)^{2}} = \sqrt{41 + 10\sqrt{7}}$

$\displaystyle AB = \sqrt{41 + 10\sqrt{7}} \approx 8.21$

To illustrate how to determine the correct length, draw a perpendicular segment from $\displaystyle R$ to $\displaystyle \overline{PA}$, calling the point of intersection $\displaystyle X$.

$\displaystyle \overline{RX}$ divides the trapezoid into Rectangle $\displaystyle TRXP$ and right triangle $\displaystyle \bigtriangleup RXA$ .

Opposite sides of a rectangle are congruent, so $\displaystyle PX = TR = 40$.

$\displaystyle m \angle TRA = 150 ^{\circ }$. The two angles of a trapezoid along the same leg - in particular, $\displaystyle \angle TRA$ and $\displaystyle \angle RAP$ - are supplementary, so 

$\displaystyle m \angle RAP = 180 ^{\circ } - m \angle TRA$

$\displaystyle = 180 ^{\circ } - 150 ^{\circ }$

$\displaystyle = 30 ^{\circ }$

By the 30-60-90 Triangle Theorem,

$\displaystyle XA = RX\cdot \sqrt{3}$

Opposite sides of a rectangle are congruent, so $\displaystyle RX= TP = 30$, and

$\displaystyle XA = 30 \sqrt{3}$

$\displaystyle \approx 30 \cdot 1.7321$

$\displaystyle \approx 30 \cdot 1.7321$

$\displaystyle \approx 52$

$\displaystyle PA = PX + XA \approx 40+ 52 \approx 92$

$\displaystyle \overline{TA}$ is the hypotenuse of right triangle $\displaystyle \bigtriangleup TPA$, so by the Pythagorean Theorem, its length can be calculated to be

$\displaystyle TA = \sqrt{ (TP )^{2}+ (PA)^{2}}$

Set $\displaystyle TP = 30$ and $\displaystyle PA = 92$:

$\displaystyle TA = \sqrt{ 30 ^{2}+ 92^{2}}$

$\displaystyle = \sqrt{ 900 + 8,464 }$

$\displaystyle = \sqrt{9,364 }$

$\displaystyle \approx 97$

To illustrate how to determine the correct length, draw a perpendicular segment from $\displaystyle R$ to $\displaystyle \overline{PA}$, calling the point of intersection $\displaystyle X$.

$\displaystyle \overline{RX}$ divides the trapezoid into Rectangle $\displaystyle TRXP$ and right triangle $\displaystyle \bigtriangleup RXA$ .

Opposite sides of a rectangle are congruent, so $\displaystyle PX = TR = 40$.

$\displaystyle m \angle TRA = 120 ^{\circ }$. The two angles of a trapezoid along the same leg - in particular, $\displaystyle \angle TRA$ and $\displaystyle \angle RAP$ - are supplementary, so 

$\displaystyle m \angle RAP = 180 ^{\circ } - m \angle TRA$

$\displaystyle = 180 ^{\circ } - 120 ^{\circ }$

$\displaystyle = 60 ^{\circ }$

By the 30-60-90 Triangle Theorem,

$\displaystyle XA = \frac{RX}{ \sqrt{3} }$

Opposite sides of a rectangle are congruent, so $\displaystyle RX= TP = 30$, and

$\displaystyle XA = \frac{RX}{ \sqrt{3} }$

$\displaystyle \approx \frac{30 }{1.7321}$

$\displaystyle \approx 17.3$

$\displaystyle PA = PX + XA \approx 40+ 17.3 \approx 57.3$

$\displaystyle \overline{TA}$ is the hypotenuse of right triangle $\displaystyle \bigtriangleup TPA$, so by the Pythagorean Theorem, its length can be calculated to be

$\displaystyle TA = \sqrt{ (TP )^{2}+ (PA)^{2}}$

Set $\displaystyle TP = 30$ and $\displaystyle PA = 57$:

$\displaystyle TA = \sqrt{ 30 ^{2}+ 57.3^{2}}$

$\displaystyle = \sqrt{ 900 + 3,283}$

$\displaystyle = \sqrt{ 4,183}$

$\displaystyle \approx 65$

To illustrate how to determine the correct length, draw a perpendicular segment from $\displaystyle R$ to $\displaystyle \overline{PA}$, calling the point of intersection $\displaystyle X$.

$\displaystyle \overline{RX}$ divides the trapezoid into Rectangle $\displaystyle TRXP$ and right triangle $\displaystyle \bigtriangleup RXA$ .

Opposite sides of a rectangle are congruent, so $\displaystyle PX = TR = 40$.

$\displaystyle m \angle TRA = 135 ^{\circ }$. The two angles of a trapezoid along the same leg - in particular, $\displaystyle \angle TRA$ and $\displaystyle \angle RAP$ - are supplementary, so 

$\displaystyle m \angle RAP = 180 ^{\circ } - m \angle TRA$

$\displaystyle = 180 ^{\circ } - 135 ^{\circ }$

$\displaystyle = 45^{\circ }$

By the 45-45-45 Triangle Theorem,

$\displaystyle XA = RX = TP =30$

and

$\displaystyle PA = PX + XA = 40+ 30 = 70$

$\displaystyle \overline{TA}$ is the hypotenuse of right triangle $\displaystyle \bigtriangleup TPA$, so by the Pythagorean Theorem, its length can be calculated to be

$\displaystyle TA = \sqrt{ (TP )^{2}+ (PA)^{2}}$

Set $\displaystyle TP = 30$ and $\displaystyle PA = 70$:

$\displaystyle TA = \sqrt{ 30 ^{2}+ 70^{2}}$

$\displaystyle = \sqrt{ 900 +4,900}$

$\displaystyle = \sqrt{ 5,800}$

$\displaystyle \approx 76$