We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Algebra 1 : Number Lines and Absolute Value

Study concepts, example questions & explanations for Algebra 1

Create An Account

All Algebra 1 Resources

10 Diagnostic Tests 557 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Number Lines And Absolute Value

Plot the fraction $-\frac{7}{3}$ on the number line.

Possible Answers:

Question_11_incorrect_2

Question_11_incorrect_1

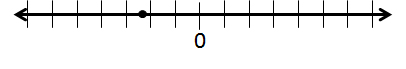
Question_11_correct

Question_11_incorrect_3

Correct answer:

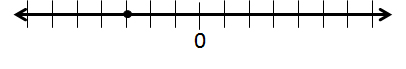
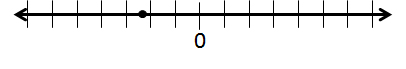
Question_11_correct

Explanation:

The fraction $-\frac{7}{3}$ is less than and greater than , so it must fall between those points on the number line. Negative numbers are to the left of while positive numbers are to the right.

$-\frac{7}{3}=-2\frac{1}{3}$

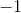
Because $\frac{1}{3}$ is less than $\frac{1}{2}$ , the point must be closer to than .

Report an Error

Example Question #1 : How To Find Absolute Value

What number or numbers have absolute value ?

Possible Answers:

-7,-14,-21,-28...

No such numbers exist.

-7,7

Correct answer:

No such numbers exist.

Explanation:

The absolute value of every real number is nonnegative, so no number with absolute value can exist.

Report an Error

Example Question #2 : How To Find Absolute Value

What number or numbers have absolute value ?

Possible Answers:

$\left \{ -13, -26, -39, -52,...\right \}$

No such numbers exist.

-13, 13

Correct answer:

No such numbers exist.

Explanation:

The absolute value of every real number is nonnegative, so no number with absolute value can exist.

Report an Error

Example Question #2 : How To Find Absolute Value

What number or numbers have absolute value 29?

Possible Answers:

No such number exists.

-29, 29

$\left \{ -29, -58,-87,-116,...\right \}$

Correct answer:

-29, 29

Explanation:

The absolute value of any positive number is the number itself, so 29 has 29 as an absolute value. Also, the absolute value of a negative number is its (positive) opposite, so also has 29 as an absolute value.

Report an Error

Example Question #4 : How To Find Absolute Value

What number or numbers have absolute value 11?

Possible Answers:

$\left \{ -11, -22,-33,-44,-55,...\right \}$

No such numbers exist.

-11,11

Correct answer:

-11,11

Explanation:

The absolute value of any positive number is the number itself, so 11 has 11 as an absolute value. Also, the absolute value of a negative number is its (positive) opposite, so also has 11 as an absolute value.

Report an Error

Example Question #1 : How To Find Absolute Value

Evaluate the expression.

$\small 3(\frac{(8-10)^2}{\left | 8-10 \right |})$

Possible Answers:

Correct answer:

Explanation:

$\small 3(\frac{(8-10)^2}{\left | 8-10 \right |})$

First, simplify the terms in parentheses and absolute value.

$3(\frac{-2^2}{\left | -2 \right |})$

Remember that the absolute value of a negative term is positive.

$3(\frac{4}{2})$

Multiply and simplify.

$\frac{3*4}{2}=\frac{12}{2}=6$

Report an Error

Example Question #4 : How To Find Absolute Value

Solve for .

$-3\left | p+2 \right |=-12$

Possible Answers:

p=2, -6

p=-2,6

p=-2,-6

A solution does not exist.

p=2,6

Correct answer:

p=2, -6

Explanation:

Divide both sides by .

$\frac{-3\left | p+2 \right |}{-3}=\frac{-12}{-3}$

$\left | p+2 \right |=4$

Remove the absolute value brackets by setting the expression equal to both the positive and negative values of 4:

p+2=4

p=2

p+2=-4

p=-6

Report an Error

Example Question #5 : How To Find Absolute Value

Mr. Smith and his wife went on a trip, they travelled miles towards their destination, however on the way there they had to turn around and drive miles away from their destination to get Mr. Smith's wallet from the store. After getting his wallet they drove more miles to reach their destination. What is the total number of miles that the family covered?

Possible Answers:

$25\:miles$

Not enough information.

$45\:miles$

$40\:miles$

$50\:miles$

Correct answer:

$50\:miles$

Explanation:

Even though the Smiths travelled backwards you still have to add the positive number to the equation. So it looks like this:

Report an Error

Example Question #9 : Number Lines And Absolute Value

Simplify the following equation:

$\left | -9\right |-\left | 4\right |$

Possible Answers:

Correct answer:

Explanation:

It is important to understand that the absolute value is the distance from a number is.

To simply this equation you need to simplify the absolute values first.

$\left | -9\right |=9$

$\left | 4\right |=4$

Then simplify the function

9-4=5

Report an Error

Example Question #2 : How To Find Absolute Value

Solve: $\left | x+3\right | = 5$

Possible Answers:

-8, 2

-8, -2

Correct answer:

-8, 2

Explanation:

In order to solve this absolute value, we will need to split up the absolute value in its positive and negative solution.

Break up the absolute value and rewrite the terms for the positive solution and solve for .

x+3=5

x=2

For the negative solution, split up the absolute value and add a negative in front of the quantity which was contained by the absolute value.

-(x+3)=5

Divide by negative one on both sides.

x+3=-5

Subtract three on both sides.

x+3-3=-5-3

Simplify both sides.

x=-8

The answers to this question are: -8, 2

Report an Error

View Algebra Tutors

Angeles
Certified Tutor

University of Central Florida, Bachelor of Science, Biomedical Sciences. University of Central Florida, Master of Science, Bi...

View Algebra Tutors

Jonathan
Certified Tutor

University of Maryland-Baltimore County, Bachelor of Science, Mathematics.

View Algebra Tutors

Steven
Certified Tutor

University of Louisville, Bachelor of Science, Mechanical Engineering. University of Phoenix-Louisville Campus, Master of Eng...

All Algebra 1 Resources

10 Diagnostic Tests 557 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Spanish Tutors in Chicago, Chemistry Tutors in Phoenix, ACT Tutors in San Francisco-Bay Area, French Tutors in Los Angeles, Reading Tutors in Denver, GRE Tutors in Washington DC, Biology Tutors in Miami, ACT Tutors in Seattle, ISEE Tutors in Los Angeles, SSAT Tutors in Seattle

Popular Courses & Classes

MCAT Courses & Classes in Washington DC, LSAT Courses & Classes in New York City, Spanish Courses & Classes in Los Angeles, GMAT Courses & Classes in Los Angeles, MCAT Courses & Classes in Boston, SAT Courses & Classes in Phoenix, LSAT Courses & Classes in Phoenix, GMAT Courses & Classes in Miami, SSAT Courses & Classes in Chicago, SAT Courses & Classes in Houston

Popular Test Prep

ISEE Test Prep in Washington DC, ISEE Test Prep in Atlanta, GRE Test Prep in Phoenix, SAT Test Prep in Los Angeles, SAT Test Prep in New York City, ACT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Denver, GMAT Test Prep in Los Angeles, ISEE Test Prep in Seattle, GMAT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra 1 : Number Lines and Absolute Value

Study concepts, example questions & explanations for Algebra 1

All Algebra 1 Resources

Example Questions

Example Question #1 : Number Lines And Absolute Value

Example Question #1 : How To Find Absolute Value

Example Question #2 : How To Find Absolute Value

Example Question #2 : How To Find Absolute Value

Example Question #4 : How To Find Absolute Value

Example Question #1 : How To Find Absolute Value

Example Question #4 : How To Find Absolute Value

Example Question #5 : How To Find Absolute Value

Example Question #9 : Number Lines And Absolute Value

Example Question #2 : How To Find Absolute Value

All Algebra 1 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: