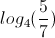We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Simplifying Logarithms

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Multiplying And Dividing Logarithms

Rewrite the following logarithmic expression in expanded form (i.e. as a sum and/or difference):

$ln \left(\frac{x^{3}y^{-2}}{2z^{4}}\right)$

Possible Answers:

3ln(x) -2ln(y) - ln(2) - 4 ln(z)

3ln(x) -2ln(y) + ln(2) + 4ln(z)

3ln(x) -2ln(y) -8ln(z)

3ln(x) + 2ln(y) - ln(2) - 4ln(z)

3ln(x) - 2ln(y) -ln(2) + 4ln(z)

Correct answer:

3ln(x) -2ln(y) - ln(2) - 4 ln(z)

Explanation:

By logarithmic properties:

$ln(x^{4}) = 4ln (x)$ ;

$ln(y^{-2})= -2ln(y)$

$\frac{1}{2z^{4}} = -ln(2) - 4ln(z)$

Combining these three terms gives the correct answer:

3ln(x) -2ln(y) - ln(2) - 4 ln(z)

Report an Error

Example Question #2 : Simplifying Logarithms

Which of the following is equivalent to

$\log(4000)$ ?

Possible Answers:

2000

$3\log4$

$3 + \log4$

$10 + \log4$

Correct answer:

$3 + \log4$

Explanation:

Recall that log implies base if not indicated.Then, we break up $4000 = 4\cdot 1000$ . Thus, we have $\log(4 \cdot 1000)$ .

Our log rules indicate that

$\log(ab) = \log(a) + \log(b)$ .

So we are really interested in,

$\log(4) + \log(1000)$ .

Since we are interested in log base , we can solve $\log(1000)$ without a calculator.

We know that 1000=10^3 , and thus by the definition of log we have that $\log(1000) = 3$ .

Therefore, we have $\log(4) + 3$ .

Report an Error

Example Question #3 : Multiplying And Dividing Logarithms

Find the value of the Logarithmic Expression.

$\log_{3} \frac{1}{81}$

Possible Answers:

Correct answer:

Explanation:

Use the change of base formula to solve this equation.

$Log_{_{3}} \frac{1}{81}$

$y = Log_{3} \frac{1}{81}$

$3^{y} = \frac{1}{81}$

$3^{^{y}} = 3^{-4}$

y = -4

Report an Error

Example Question #3 : Simplifying Logarithms

What is another way of expressing the following?

$\small 3\log(2)$

Possible Answers:

$\small \log (6)$

$\small \log (5)$

$\small \small \log (\frac{2}{3})$

$\small \log (9)$

$\small \log (8)$

Correct answer:

$\small \log (8)$

Explanation:

Use the rule

$\small a\times \log (b)= \log (b^{a})$

$\small \log (2^{3})=\log (8)$

Report an Error

Example Question #4 : Simplifying Logarithms

Expand this logarithm: $\log_{10}8x^4y$

Possible Answers:

$\log_{10}(8+y+x^4)$

$\log_{10}8y+4\log_{10}x$

$\log_{10}8+4\log_{10}x+\log_{10}y$

$\log_{10}y+\log_{10}x^4 +8$

$\log_{10}8+\log_{10}x^4+\log_{10}y$

Correct answer:

$\log_{10}8+4\log_{10}x+\log_{10}y$

Explanation:

In order to solve this problem you must understand the product property of logarithms $\log_{10}uv=\log_{10}u+\log_{10}v$ and the power property of logarithms $\log_{10}u^n=n\log_{10}u$ . Note that these apply to logs of all bases not just base 10.

$\log_{10}8x^4y$

log of multiple terms is the log of each individual one:

$\log_{10}8+\log_{10}x^4+\log_{10}y$

now use the power property to move the exponent over:

$\log_{10}8+4\log_{10}x+\log_{10}y$

Report an Error

Example Question #6 : Multiplying And Dividing Logarithms

Which of the following is equivalent to $log(\frac{a^2b^3}{x^{-3}})$ ?

Possible Answers:

2log(a)+log(b-x)^3

log(2a)+log(3b)+log(3x)

2log(a)+3log(b-x)

2log(a)+3log(b)-3log(x)

2log(a)+3log(b)+3log(x)

Correct answer:

2log(a)+3log(b)+3log(x)

Explanation:

We can rewrite the terms of the inner quantity. Change the negative exponent into a fraction.

$x^{-3} = \frac{1}{x^3}$

$\frac{a^2b^3}{x^{-3}} = a^2b^3 \div \frac{1}{x^3}= a^2b^3 \times \frac{x^3}{1} =a^2b^3x^3$

This means that:

$log(\frac{a^2b^3}{x^{-3}}) = log(a^2b^3x^3)$

Split up these logarithms by addition.

log(a^2b^3x^3) = log(a^2)+log(b^3)+log(x^3)

According to the log rules, the powers can be transferred in front of the logs as coefficients.

The answer is: 2log(a)+3log(b)+3log(x)

Report an Error

Example Question #5 : Simplifying Logarithms

Many textbooks use the following convention for logarithms:

$log(x) = log_{10}(x)$

ln(x) = log_e(x)

lg(x)=log_2(x)

Solve:

$lg(\frac{4096}{16384})$

Possible Answers:

Correct answer:

Explanation:

Remembering the rules for logarithms, we know that $log_a(\frac{b}{c}) = log_ab - log_ac$ .

This tells us that $lg(\frac{4096}{16384})=lg(4096)-lg(16384)$ .

This becomes 12 - 14 , which is .

Report an Error

Example Question #1 : Adding And Subtracting Logarithms

Simplify the following logarithmic expression:

$log_{3}81 - log_{5} (\frac{1}{25}) + log_{7} 7^{\frac{3}{2}}$

Possible Answers:

$\frac{21}{2}$

$\frac{7}{2}$

$\frac{15}{2}$

Correct answer:

$\frac{15}{2}$

Explanation:

Each term can be simplified as follows:

$log_{3}81 = log_{3} 3^{4} = 4$

$- log_{5} (\frac{1}{25}) = - log_{5} (5)^{-2} = -(-2) = 2$

$log_{7} 7^{\frac{3}{2}} = \frac{3}{2}$

Combining these gives the answer: $\frac{15}{2}$

Report an Error

Example Question #1 : Logarithms

Simplify the expression using logarithmic identities.

log_47-log_45

Possible Answers:

$log_4(\frac{5}{7})$

log_4(35)

The expression cannot be simplified

$log_4(\frac{7}{5})$

log_4(2)

Correct answer:

$log_4(\frac{7}{5})$

Explanation:

The logarithm of a fraction is equal to the logarithm of the numerator minus the logarithm of the denominator.

$log_A(\frac{B}{C})=log_AB-log_AC$

If we encounter two logarithms with the same base, we can likely combine them. In this case, we can use the reverse of the above identity.

$log_AB-log_AC=log_A(\frac{B}{C})$

$A=4,\ B=7,\ C=5$

$log_47-log_45=log_4(\frac{7}{5})$

Report an Error

Example Question #1 : Adding And Subtracting Logarithms

Use logarithmic properties to simplify this expression:

$log(4x)+log\left(\frac{1}{2}\right)-log(y^{2})$

Possible Answers:

$log(2xy^{2})$

$log\left(\frac{8x}{y^{2}}\right)$

$log\left(\frac{2x^{2}}{y^{2}}\right)$

$log\left(\frac{4x}{y^{2}}\right)$

$log\left(\frac{2x}{y^{2}}\right)$

Correct answer:

$log\left(\frac{2x}{y^{2}}\right)$

Explanation:

Use the sum/product rule to combine the first 2 terms:

$log\left(4x\ast \frac{1}{2}\right)-log(y^{2})=log(2x)-log(y^{2})$

Use the difference/quotient rule to combine the remaining terms:

$log\left(\frac{2x}{y^{2}}\right)$

Report an Error

View Algebra 2 Tutors

Isabella
Certified Tutor

Iowa State University, Bachelor of Science, Mathematics.

View Algebra 2 Tutors

Margaret
Certified Tutor

View Algebra 2 Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GMAT Tutors in Philadelphia, Spanish Tutors in Denver, ACT Tutors in Seattle, Spanish Tutors in Seattle, ACT Tutors in Phoenix, Biology Tutors in San Diego, SAT Tutors in Seattle, GRE Tutors in San Diego, Statistics Tutors in Chicago, Spanish Tutors in New York City

Popular Courses & Classes

GRE Courses & Classes in Philadelphia, Spanish Courses & Classes in Chicago, ACT Courses & Classes in Seattle, ACT Courses & Classes in Phoenix, ISEE Courses & Classes in Miami, ISEE Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in Miami, SAT Courses & Classes in Philadelphia, MCAT Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Seattle

Popular Test Prep

MCAT Test Prep in Boston, GRE Test Prep in Miami, GRE Test Prep in Denver, ISEE Test Prep in Chicago, SAT Test Prep in Phoenix, ACT Test Prep in Dallas Fort Worth, ACT Test Prep in New York City, GRE Test Prep in San Francisco-Bay Area, SAT Test Prep in San Francisco-Bay Area, GRE Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra II : Simplifying Logarithms

Study concepts, example questions & explanations for Algebra II

All Algebra II Resources

Example Questions

Example Question #1 : Multiplying And Dividing Logarithms

Example Question #2 : Simplifying Logarithms

Example Question #3 : Multiplying And Dividing Logarithms

Example Question #3 : Simplifying Logarithms

Example Question #4 : Simplifying Logarithms

Example Question #6 : Multiplying And Dividing Logarithms

Example Question #5 : Simplifying Logarithms

Example Question #1 : Adding And Subtracting Logarithms

Example Question #1 : Logarithms

Example Question #1 : Adding And Subtracting Logarithms

All Algebra II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: