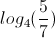All Algebra II Resources
Example Questions
Example Question #1 : Multiplying And Dividing Logarithms
Rewrite the following logarithmic expression in expanded form (i.e. as a sum and/or difference):
By logarithmic properties:

Combining these three terms gives the correct answer:
Example Question #1 : Simplifying Logarithms
Which of the following is equivalent to

Recall that log implies base 


Our log rules indicate that

So we are really interested in,

Since we are interested in log base 

We know that 

Therefore, we have 
Example Question #3 : Simplifying Logarithms
Find the value of the Logarithmic Expression.
Use the change of base formula to solve this equation.
Example Question #2 : Multiplying And Dividing Logarithms
What is another way of expressing the following?
Use the rule
Example Question #1 : Simplifying Logarithms
Expand this logarithm:
In order to solve this problem you must understand the product property of logarithms 

log of multiple terms is the log of each individual one:
now use the power property to move the exponent over:
Example Question #6 : Simplifying Logarithms
Which of the following is equivalent to 
We can rewrite the terms of the inner quantity. Change the negative exponent into a fraction.
This means that:
Split up these logarithms by addition.
According to the log rules, the powers can be transferred in front of the logs as coefficients.
The answer is:
Example Question #4 : Multiplying And Dividing Logarithms
Many textbooks use the following convention for logarithms:
Solve:
Remembering the rules for logarithms, we know that 
This tells us that 
This becomes 

Example Question #1 : Adding And Subtracting Logarithms
Simplify the following logarithmic expression:
Each term can be simplified as follows:
Combining these gives the answer:
Example Question #1 : Adding And Subtracting Logarithms
Simplify the expression using logarithmic identities.
The expression cannot be simplified
The logarithm of a fraction is equal to the logarithm of the numerator minus the logarithm of the denominator.
If we encounter two logarithms with the same base, we can likely combine them. In this case, we can use the reverse of the above identity.
Example Question #1 : Adding And Subtracting Logarithms
Use logarithmic properties to simplify this expression:
Use the sum/product rule to combine the first 2 terms:
Use the difference/quotient rule to combine the remaining terms:
Certified Tutor
Certified Tutor
All Algebra II Resources