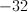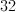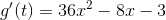We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus AB : Derivative as a function

Study concepts, example questions & explanations for AP Calculus AB

Create An Account

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Derivative As A Function

A gun sends a bullet straight up with a launch velocity of 220 ft/s. It reaches a height of $s=220t-16t^2$ after seconds. What's the acceleration in $m/s^{2}$ of the block after it has been ejected?

Possible Answers:

Correct answer:

Explanation:

Since $a=\frac{ds^2}{dt^2}$ , by differentiating the position function twice, we see that acceleration is constant and $-32\ m/s^{2}$ . Acceleration, in this case, is gravity, which makes sense that it should be a constant value!

Report an Error

Example Question #11 : Calculus I — Derivatives

The speed of a car traveling on the highway is given by the following function of time:

f(t) = 5t^2+2t

Consider a second function:

g(t) = 10t+2

What can we conclude about this second function?

Possible Answers:

It represents the rate at which the speed of the car is changing.

It represents the change in distance over a given time .

It has no relation to the previous function.

It represents the total distance the car has traveled at time .

It represents another way to write the car's speed.

Correct answer:

It represents the rate at which the speed of the car is changing.

Explanation:

Notice that the function g(t) is simply the derivative of f(t) with respect to time. To see this, simply use the power rule on each of the two terms.

f'(t) = (2)(5)t + 2 = g(t)

Therefore, g(t) is the rate at which the car's speed changes, a quantity called acceleration.

Report an Error

Example Question #1 : Corresponding Characteristics Of Graphs Of ƒ And ƒ'

Find the critical numbers of the function,

$f(x)=\frac{1+x^2}{x}$

Possible Answers:

$x =\left \{ -1,0,1\right \}$

$x =\left \{ -1\right \}$

$x =\left \{ 1\right \}$

$x =\left \{ -1,1\right \}$

Correct answer:

$x =\left \{ -1,1\right \}$

Explanation:

$f(x)=\frac{1+x^2}{x}$

1) Recall the definition of a critical point:

The critical points of a function f(x) are defined as points (a,f(a)) , such that x=a is in the domain of f(x) , and at which the derivative f'(a) is either zero or does not exist. The number x=a is called a critical number of f(x) .

2) Differentiate ,

$f'(x)=\frac{d}{dx}\left(\frac{1+x^2}{x} \right )=\frac{d}{dx}\left(\frac{1}{x}+x \right )=-\frac{1}{x^2}+1$

3) Set to zero and solve for ,

$f'(x)=-\frac{1}{x^2}+1= 0$

$\frac{1}{x^2}=1$

The critical numbers are,

$x =\left \{ -1,1\right \}$

We can also observe that the derivative does not exist at x = 0 , since the $-\frac{1}{x^2}$ term would be come infinite. However, is not a critical number because the original function f(x) is not defined at x=0 . The original function is infinite at x=0 , and therefore x = 0 is a vertical asymptote of f(x) as can be seen in its' graph,

Problem 7 plot

Further Discussion

In this problem we were asked to obtain the critical numbers. If were were asked to find the critical points, we would simply evaluate the function f(x) at the critical numbers to find the corresponding function values and then write them as a set of ordered pairs,

$\left \{(-1,-2), (1,2) \right \}$

Report an Error

Example Question #2 : Corresponding Characteristics Of Graphs Of ƒ And ƒ'

The function f(x) is a continuous, twice-differentiable functuon defined for all real numbers.

If the following are true:

Which function could be f(x) ?

Possible Answers:

sin(x)

e^x

$\frac{1}{x^2}$

ln(x)

Correct answer:

ln(x)

Explanation:

To answer this problem we must first interpret our given conditions:

Implies the function is strictly increasing.
Implies the function is strictly concave down.

We note the only function given which fufills both of these conditions is lnx .

Report an Error

Example Question #3 : Corresponding Characteristics Of Graphs Of ƒ And ƒ'

A jogger leaves City at t=0 . His subsequent position, in feet, is given by the function:

$x(t) = 5t^{2} - 3t + 2$ ,

where is the time in minutes.

Find the acceleration of the jogger at t=15 minutes.

Possible Answers:

$10\ ft/min$

$10\ ft/min^{2}$

$10\ ft$

$147\ ft/min^{2}$

$147\ ft/min$

Correct answer:

$10\ ft/min^{2}$

Explanation:

The accelaration is given by the second derivative of the position function:
a(t) = f''(t)

For the given position function:

$f(t) = 5t^{2} - 3t + 2$ ,

f'(t) = 10t - 3 ,

f''(t) = 10 .

Therefore, the acceleration at t=15 minutes is $10\ ft/min^{2}$ . Again, note the units must be in $ft/min^{2}$ .

Report an Error

Example Question #2 : Derivative As A Function

On which interval(s) is the function f(x)=x^3+5x^2-8x+7 increasing and on which interval(s) is it decreasing?

Possible Answers:

Increasing: $(-\infty,\infty)$

Increasing: $(-\infty ,-4), (\frac{2}{3},\infty)$

Decreasing: $(-4,\frac{2}{3})$

Increasing: $(-\infty,\frac{-2}{3}), (4,\infty)$

Decreasing: $(\frac{-2}{3},4)$

Decreasing: $(-\infty ,-4), (\frac{2}{3},\infty)$

Increasing: $(-4,\frac{2}{3})$

Decreasing: $(-\infty,\infty)$

Correct answer:

Increasing: $(-\infty ,-4), (\frac{2}{3},\infty)$

Decreasing: $(-4,\frac{2}{3})$

Explanation:

First we must find out critical points by setting f'(x) equal to zero.

f'(x)=0=3x^2+10x-8

Then we reverse foil to get

$0=(3x-2)(x+4)\Rightarrow 3x-2=0 \and\ x+4=0$

$x=\frac{2}{3}, x=-4$

These are our critical points. We now must test values on each interval defined by our critical points in order to determine the sign of f'(x) on each interval.

Our intervals to check are

$(-\infty,-4),(-4,\frac{2}{3}),(\frac{2}{3},\infty)$

We have many choices, but let's choose $x=-5, \ x=0 ,\ x=1$

$f'(-5)=3\cdot (-5^2)+10\cdot(-5)-8=17$

$f'(0)=3\cdot0^2 +10\cdot0-8=-8$

$f'(1)=3\cdot (1^2)+10\cdot (1)-8=5$

Thus on our first interval f'(x) is positive meaning f(x) is increasing.

On our second interval f'(x) is negative meaning f(x) is decreasing.

And on our third interval f'(x) is positive meaning f(x) is increasing.

Report an Error

Example Question #1 : Relationship Between The Increasing And Decreasing Behavior Of ƒ And The Sign Of ƒ'

What does the sign of the first derivative tell us about whether a function is increasing or decreasing?

Possible Answers:

If the first derivative is negative, then the function is decreasing. If the first derivative is positive, then the function is increasing.

The sign of the first derivative does not tell us anything about whether a function is increasing or decreasing.

If the first derivative is positive, then the function is decreasing. If the first derivative is negative, then the function is increasing.

If the first derivative is negative, then the function is decreasing, but if the first derivative is positive, then the function is neither increasing nor decreasing.

Correct answer:

If the first derivative is negative, then the function is decreasing. If the first derivative is positive, then the function is increasing.

Explanation:

What does the sign of the first derivative tell us about whether a function is increasing or decreasing?

The first derivative test is used to tell whether a function is increasing or decreasing at a certain point or interval.

To use this test, first find the derivative of your function. Then, plug in the values for the point(s) and see what sign you get on your values.

If the value of your first derivative is negative, then your function is decreasing. If the value of your first derivative is positive, your original function is increasing. If your first derivative is 0, then you have a point of inflection in your original function.

Report an Error

Example Question #1 : Relationship Between The Increasing And Decreasing Behavior Of ƒ And The Sign Of ƒ'

Use the first derivative test to tell whether f(c) is increasing or decreasing when c=24.

f(c)=134c^2-325c+15

Possible Answers:

Decreasing, because our first derivative is negative.

Increasing, because our first derivative is negative.

Decreasing, because our first derivative is positive.

Increasing, because our first derivative is positive.

Correct answer:

Increasing, because our first derivative is positive.

Explanation:

Use the first derivative test to tell whether f(c) is increasing or decreasing when c=24

f(c)=134c^2-325c+15

Begin by finding the first derivative of f(c)

f'(c)=(2)134c-325=168c-325

Next, plug in 24 for c and find the sign of our first derivative.

f'(24)=268(24)-325=6107

Now, our first derivative is positive, so our original function must be increasing.

Report an Error

Example Question #3 : Derivative As A Function

Find the derivative of g(t) and tell whether g(t) is increasing or decreasing on the interval [5,6].

g(t)=-12x^3+4x^2+3x

Possible Answers:

g'(t)=-36x^2+32x+3

Increasing

g'(t)=-36x^2+8x+3

Decreasing

g'(t)=36x^2-32x-3

Decreasing

g'(t)=36x^2-8x-3

Increasing

Correct answer:

g'(t)=-36x^2+8x+3

Decreasing

Explanation:

Find the derivative of g(t) and tell whether g(t) is increasing or decreasing on the interval [5,6]

g(t)=-12x^3+4x^2+3x

First, find the derivative by decreasing each exponent by 1 and multiplying the coefficient by that number.

g'(t)=-(3)12x^2+2(4)x+3=-36x^2+8x+3

Next, plug in our two endpoints of our interval to see what the sign of g'(t) is.

g'(t)=-36x^2+8x+3

g'(5)=-36(5)^2+8(5)+3=-900+40+3=-857

g'(6)=-36(6)^2+8(6)+3=-1296+48+3=-1245

Now, clearly these are both negative, and every point between them will be negative. This means that function g(t) is decreasing on this interval.

Report an Error

Example Question #1 : Relationship Between The Increasing And Decreasing Behavior Of ƒ And The Sign Of ƒ'

Tell whether f is increasing or decreasing when . How do you know?

f(x)=14x^6-3x^5-137x^3+26x^2-12x-20

Possible Answers:

f(x) is decreasing, because f'(-12)> 0

f(x) is increasing, because f'(-12)<0

f(x) is decreasing, because f'(-12)<0

f(x) is increasing, because f'(-12)> 0

Correct answer:

f(x) is decreasing, because f'(-12)<0

Explanation:

Tell whether f is increasing or decreasing when . How do you know?

f(x)=14x^6-3x^5-137x^3+26x^2-12x-20

To test for increasing/decreasing, we need to find the first derivative.

In this case, we can use the power rule to do all our differentiation.

Power rule:

$\frac{d}{dx}x^n=(n)x^{n-1}$

We will use this on each term in order to find our first and then second derivative.

For each term, we will decrease the exponent by 1, and then multiply by the original exponent.

f(x)=14x^6-3x^5-137x^3+26x^2-12x-20

f'(x)=(6)14x^5-(5)3x^4-(3)137x^2+(2)26x-12

f'(x)=84x^5-15x^4-411x^2+52x-12

Now, we need to find the sign of f'(-12). This will tell us if it is increasing or decreasing.

f'(-12)=84(-12)^5-15(-12)^4-411(-12)^2+52(-12)-12

f'(-12)=-20901890-311040-59184-624-12=-21,272,750

So, we get

f'(-12)=-21,272,750

So,

f(x) is decreasing, because f'(-12)<0

Report an Error

View AP Calculus AB Tutors

Michelle
Certified Tutor

University of Nevada-Las Vegas, Bachelor of Science, Mathematics.

View AP Calculus AB Tutors

Yucheng
Certified Tutor

The University of Texas at Austin, Bachelor of Science, Mechanical Engineering.

View AP Calculus AB Tutors

Mohammad
Certified Tutor

Rutgers University-New Brunswick, Bachelor of Science, Mathematics. Rutgers University-New Brunswick, Master of Science, Stat...

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ACT Tutors in Atlanta, Chemistry Tutors in Boston, SAT Tutors in Washington DC, French Tutors in Denver, ISEE Tutors in Philadelphia, Computer Science Tutors in Philadelphia, SAT Tutors in Chicago, GMAT Tutors in San Diego, Calculus Tutors in Los Angeles, LSAT Tutors in Los Angeles

Popular Courses & Classes

GMAT Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in Boston, GRE Courses & Classes in Houston, LSAT Courses & Classes in Houston, MCAT Courses & Classes in San Diego, MCAT Courses & Classes in Boston, ACT Courses & Classes in Phoenix, ACT Courses & Classes in New York City, GRE Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Dallas Fort Worth

Popular Test Prep

ACT Test Prep in New York City, GMAT Test Prep in San Diego, ACT Test Prep in Phoenix, SSAT Test Prep in Atlanta, SAT Test Prep in Denver, GRE Test Prep in Philadelphia, SSAT Test Prep in Dallas Fort Worth, GRE Test Prep in Houston, LSAT Test Prep in New York City, ISEE Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus AB : Derivative as a function

Study concepts, example questions & explanations for AP Calculus AB

All AP Calculus AB Resources

Example Questions

Example Question #1 : Derivative As A Function

Example Question #11 : Calculus I — Derivatives

Example Question #1 : Corresponding Characteristics Of Graphs Of ƒ And ƒ'

Example Question #2 : Corresponding Characteristics Of Graphs Of ƒ And ƒ'

Example Question #3 : Corresponding Characteristics Of Graphs Of ƒ And ƒ'

Example Question #2 : Derivative As A Function

Example Question #1 : Relationship Between The Increasing And Decreasing Behavior Of ƒ And The Sign Of ƒ'

Example Question #1 : Relationship Between The Increasing And Decreasing Behavior Of ƒ And The Sign Of ƒ'

Example Question #3 : Derivative As A Function

Example Question #1 : Relationship Between The Increasing And Decreasing Behavior Of ƒ And The Sign Of ƒ'

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: