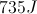The forces acting on the child are the force of gravity and the upward force provided by the child himself. Choosing the upward direction as positive, Newton's second law applied to the child gives the following equation.

\(\displaystyle \Sigma F_y=F_c-mg=0\)

\(\displaystyle F_c=mg=(25\ \text{kg})(9.8\ \frac{m}{s^2})=245\ \text{N}\)

To calculate the work done by the child to bring himself three meters up the tree, we use the work equation below.

\(\displaystyle W=F_c\cdot d=(245\ \text{N})(3\ \text{m})=735\ \text{J}\)

The net force on the box is the applied force minus the friction force, since friction acts in the direction opposite motion.

\(\displaystyle F_{net}=F_{app}-F_{friction}\)

Consequently, the net force is:

\(\displaystyle F_{net}=27N-2N = 25 N\)

The formula for work is:

\(\displaystyle W=F_{net}*d\)

Substituting in our net force and distance, we find that the work done on the box is:

\(\displaystyle W=25N(3.7m)=92.5 N\cdot m\)

\(\displaystyle W=92.5J\)

The defintion of work is:

\(\displaystyle W=F_{net}\cdot d\)

The net force on this object is:

\(\displaystyle F_{net}=F_{app}-F_{friction}\)

We can calculate this term using the given values:

\(\displaystyle F_{net}=53N-3.47N=49.53N\)

The distance is given. Substituting these values:

\(\displaystyle W=49.53 N (7.9m)=391.29 J\)

The equation of work is given by \(\displaystyle W = F\cdot d\), where \(\displaystyle F\) is force and \(\displaystyle d\) is the distance. Both the work and the force are given to us, but in vector form. In this case, we have to take the dot product of the force and distance.

When taking dot product, keep these rule in mind

\(\displaystyle i \cdot i = 1, j \cdot j = 1, k \cdot k =1\)

Every other dot proudct is equal to 0.

\(\displaystyle (8i - 2j +3k) \cdot (2i + 3j - 1k) = \\((8\cdot2)+(-2\cdot3)+(3\cdot-1) ) = 7\:J\)

Power is determined by calculating the work output per unit time. In this case, power will be the product of torque and angular velocity:

\(\displaystyle P=\tau*\omega\)

We are given values for our torque and our power output, allowing us to solve for the angualr velocity. Keep in mind that the power output is going to be 50% of the maximum.

\(\displaystyle 250W=(30N\cdot m)(\omega)\)

\(\displaystyle \omega=8.33\frac{rad}{s}\)

For this problem we can calculate the power as the product of force and velocity:

\(\displaystyle P=Fv\)

First, we need to find the velocity:

\(\displaystyle v=\frac{\Delta x}{\Delta t}=\frac{20m}{10s}=2\frac{m}{s}\)

Our force will be equal to the weight of the crate:

\(\displaystyle F=mg=(50kg)(9.8\frac{m}{s})=490N\)

Now, we can solve for power:

\(\displaystyle P=Fv=(490N)(2\frac{m}{s})=980W\)

Because the boxes are the same mass and are moving the same distance, the work done will remain the same between the two instances. Work does not depend on time:

\(\displaystyle W=Fd\)

However, when carrying the second box, the person moves more slowly. The overall time increases, which leads to a decrease in power.

\(\displaystyle P=\frac{W}{t}\)

The definition of power is:

\(\displaystyle P=\frac{W}{t}\)

The work done on the box to lift it is required in order to overcome the force of gravity. If we can find the force of gravity on the object, we can calculate the net force. The force of gravity on any object near the Earth's surface is:

\(\displaystyle F_g=mg\)

The definition of work is:

\(\displaystyle W=F_{net}d\)

We can substitute the force of gravity for the net force, resulting in the equation:

\(\displaystyle W=mgd\)

Substituting this into our power equation, we find:

\(\displaystyle P=\frac{mgd}{t}\)

Plugging in our given values and constants, we find:

\(\displaystyle P=\frac{(25 kg) (9.81 \frac{m}{s^2})(5.76m)}{15 s}\)

\(\displaystyle P=\frac{(25)(9.81)(5.76)}{15}\frac{kgm^2}{s^3}\)

\(\displaystyle P=87.36 W\)

Begin by using the following equation relating the initial and final kinetic energy and the work done on the object:

\(\displaystyle KE_i + W = KE_f\)

Then, plug in the given variables and solve for the final speed.

\(\displaystyle \frac{1}{2}mv_i^2 + Fd = \frac{1}{2}mv_f^2\)

\(\displaystyle \frac{1}{2}(25kg)(25\frac{m}{s})^2 + (250N)(13.75m) = \frac{1}{2}(25kg)v_f^2\)

Simplify terms.

\(\displaystyle 7812.5 + 3437.5 = \frac{25}{2}v_f^2\)

Isolate the final velocity and solve.

\(\displaystyle v_f = \sqrt{11250*\frac{2}{25}}\)

\(\displaystyle v_f = \sqrt{900}\)

\(\displaystyle v_f = 30\frac{m}{s}\)

You can use the motion equation and find the maximum, but it may be faster to use energy equations. Set the initial kinetic energy equal to the gravitational potential energy at the maximum height and solve for the height.

\(\displaystyle \frac{1}{2}mv^2 = mgh\)

Mass cancels.

\(\displaystyle \frac{1}{2}v^2 = gh\)

Isolate the height and solve.

\(\displaystyle h = \frac{v^2}{2g} = \frac{(32.65\frac{m}{s})^2}{2(9.8\frac{m}{s^2})} = 54.3889m\)

Round to \(\displaystyle 54m\).