All College Algebra Resources
Example Questions
Example Question #1 : Complex Numbers
Consider the following definitions of imaginary numbers:
Then,
Example Question #2 : Complex Numbers
What is the value of 
When dealing with imaginary numbers, we multiply by foiling as we do with binomials. When we do this we get the expression below:
Since we know that 


Example Question #3 : Complex Numbers
What is the value of 
Recall that the definition of imaginary numbers gives that 

Example Question #5 : Basic Operations With Complex Numbers
Add:
When adding complex numbers, add the real parts and the imaginary parts separately to get another complex number in standard form.
Adding the real parts gives 

Example Question #1 : How To Find Value With A Number Line
Divide:
The answer must be in standard form.
Multiply both the numerator and the denominator by the conjugate of the denominator which is 
The numerator after simplification give us
The denominator is equal to
Hence, the final answer in standard form =
Example Question #162 : How To Write Expressions And Equations
Divide:
Answer must be in standard form.
Multiply both the numerator and the denominator by the conjugate of the denominator which is 
This is equal to
Since 


When you then cancel the negatives in both numerator and denominator (remember that 



Example Question #4691 : Algebra Ii
Evaluate:
Use the FOIL method to simplify. FOIL means to mulitply the first terms together, then multiply the outer terms together, then multiply the inner terms togethers, and lastly, mulitply the last terms together.
The imaginary 
Write the terms for 
Replace 
Example Question #71 : Imaginary Numbers
The answer is not present.
Combine like terms:
Distribute:
Combine like terms:
Example Question #7 : Complex Numbers
Rationalize the complex fraction:
To rationalize a complex fraction, multiply numerator and denominator by the conjugate of the denominator.
Example Question #121 : Review And Other Topics
Multiply:
Use FOIL to multiply the two binomials.
Recall that FOIL stands for Firsts, Outers, Inners, and Lasts.
Remember that
Certified Tutor
All College Algebra Resources






























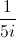
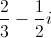




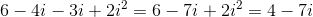
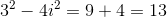

















![=i[(1)(2)+(1)(-i)+(i)(2)+(i)(-i)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/391457/gif.latex)
![=i[2-i+2i-i^2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/391458/gif.latex)
![=i[2+i-i^2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/391459/gif.latex)








































