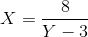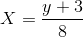In \(\displaystyle Y=8X+3\), if we're solving for x, we first need to get the "x" term isolated. We do this by subtracting 3 from both sides so:

\(\displaystyle Y=8X+3\)

becomes

\(\displaystyle Y-3=8X\)

Now we divide both sides by 8

\(\displaystyle \frac{Y-3}{8}=X\)

Re-written the answer becomes

\(\displaystyle X=\frac{Y-3}{8}\)

Since this problems has 2 variables (D-dimes and Q-quarters) we need 2 equations. Because Larry has 14 coins, the first equation can be written as:

\(\displaystyle D+Q=14\)

The value of those coins equals $2.60 or 260 cents. If Dimes are worth 10C and quarters are 25C, the next equation can be written as

\(\displaystyle 10D+25Q=260\)

To solve this write both equations on top of each other

\(\displaystyle D+Q=14\)

\(\displaystyle 10D+25Q=260\)

Now we eliminate 1 variable by multiplying 1 equation by the lowest common denominator (as a negative) and adding the equations together.

\(\displaystyle -10(D+Q=14)\)   becomes

\(\displaystyle -10D-10Q=-140\)

adding the equations

\(\displaystyle -10D-10Q=-140\)

    \(\displaystyle 10D+25Q=260\)

-----------------------------------

                  \(\displaystyle 15Q=120\)

now we solve for Q.

\(\displaystyle Q=\frac{120}{15}=8\)

Since we know Q, now we plug it back in to an equation and find D

\(\displaystyle D+8=14 --> D=6\)

Larry has 6 dimes and 8 quarters

There are two ways to solve for x and y in a pair of equations. One way is to add the two equations together and eliminate one of the variables. It may be necessary to multiply one equation by a positive or negative number in order to cancel out one of the variables. The second way is to pick one of the equations and solve for one of the variables. Let's pick the top equation and solve for x:

\(\displaystyle 2x+4y=24\)

\(\displaystyle 2x+4y (-4y)=24 (-4y)\)

\(\displaystyle 2x=24-4y\)

\(\displaystyle 2x/2=24/2-4y/2\)

\(\displaystyle x=12-2y\)

Now substitute x on the other (bottom) equation:

\(\displaystyle 4x-3y=-7\)

\(\displaystyle 4(12-2y)-3y=-7\)

\(\displaystyle 48-8y-3y=-7\)

\(\displaystyle 48-11y=-7\)

\(\displaystyle 48-11y(-48)=-7(-48)\)

\(\displaystyle -11y=-55\)

\(\displaystyle -11y/-11=-55/-11\)

\(\displaystyle {\color{Red} y=5}\)

Now, since we know the value of y, use either equation and "plug in" the value of y:

\(\displaystyle 2x+4y=24\)

\(\displaystyle 2x-4({\color{Red} 5})=24\)

\(\displaystyle 2x+20=24\)

\(\displaystyle 2x+20(-20)=24(-20)\)

\(\displaystyle 2x=4\)

\(\displaystyle 2x/2=4/2\)

\(\displaystyle {\color{Red} x=2}\)

To check your answers, you can plug in both answers to either equation, and since they are equations, if both sides are equal, your answers are correct.

There are 2 ways to solve this set of equations. First, you can solve for one of the variables, then substitute that value for the variable in the other equation. The other way is to add the equations together (combine), and to do this, sometimes multiplying one of the equation by a positive or negative number is required. Let's see how we can do this:  

Remember the key is to add the two equations together and eliminate one of the variables:

   \(\displaystyle 2x+4y=22\)

\(\displaystyle -2x+2y=2\)

Look at the x and y variables. Notice how if we added the two equations together, we can eliminate the x variable and we can thus solve for y:

So now, add the two equations together:

\(\displaystyle 6y=24\)

We got this buy adding 4y + 2y and 22+2. Now let's divide the equation by 6, so we can solve the value of y.

\(\displaystyle 6y/6=24/6\)     so

\(\displaystyle {\color{Red} y=4}\)       

Now plug the known value of y into either of the two equations. Let's use the top equation. Remember it doesn't matter which equation you pick to solve for x:

\(\displaystyle 2x+4(4)=22\)

\(\displaystyle 2x+16(-16)=22(-16)\)

\(\displaystyle 2x/2=6/2\)

\(\displaystyle {\color{Red} x=3}\)   

If you want to double-check your answers, just insert your values of x and y into the equation, and remember that since it's an equation, both sides will be equal.

There are 2 ways to solve this set of equations. First, you can solve for one of the variables, then substitute that value for the variable in the other equation. The other way is to add the equations together (combine), and to do this, sometimes multiplying one of the equation by a positive or negative number is required. Let's see how we can do this:  

Remember the key is to add the two equations together and eliminate one of the variables.  

\(\displaystyle x+y=7\)

\(\displaystyle x-y=1\)

so let's look at the pair of equations. Both x's are positive, so we'd have to multiply one of the equations by -1 to eliminate the x variable. Let's look at the y. One is positive, and one is negative, so adding the equations as they are would eliminate y. So after you add the two equations together, you will get:

\(\displaystyle 2x=8\) 

The y was eliminated as you can see, so now we can solve for x. Let's divide both sides by 2 to isolate the x variable:

\(\displaystyle 2x/2=8/2\)

\(\displaystyle {\color{Red} x=4}\)

Now that we have the value of x, all you have to do is plug the value of x into either of the two equations to solve for y. Let's pick the top equation:

\(\displaystyle (4)+y=7\)

Now subtract 4 from each side to isolate the y and solve for y:

\(\displaystyle 4+y(-4)=7(-4)\)

\(\displaystyle {\color{Red} y=3}\)

If you want to check your answers, just plug the values you got for x and y into either of the pair of equations. Since they are equations, both sides will be equal if you found the correct values for x and y.

There are 2 ways to solve this set of equations. First, you can solve for one of the variables, then substitute that value for the variable in the other equation. The other way is to add the equations together (combine), and to do this, sometimes multiplying one of the equation by a positive or negative number is required. Let's see how we can do this:  Remember the key is to add the two equations together and eliminate one of the variables. Let's look at the pair of equations. With either of the variables, since both x an y are positive and negative, you just have to multiply one of the equations in order to eliminate one of the variables. Let's eliminate y.  

   \(\displaystyle 3x-4y=-18\)

\(\displaystyle -6x+2y=0\)    

In order to eliminate y, we will have to multiply the bottom equation by 2. When adding the two equations together, -4y and 4y will then cancel each other out, allowing you to solve for x.

\(\displaystyle 3x-4y=-18\)

\(\displaystyle -6x(2)+2y(2)=0(2)\)

So now this is the new pair of equations, where y is eliminated. Now just add the two equations together:

      \(\displaystyle 3x-4y=-18\)

\(\displaystyle -12x+4y=0\)

So the resulting equation after adding these equations together is:

\(\displaystyle -9x=-18\)

Now divide both sides by -9 to solve for x:

\(\displaystyle -9x/-9=-18/-9\)

\(\displaystyle {\color{Red} x=2}\)

Now just plug in the value of x into either of the two equations. Let's pick the top equation:

\(\displaystyle 3(2)-4y=-18\)

\(\displaystyle 6-4y=-18\) 

Now subtract six from both sides to isolate the y:

\(\displaystyle 6-4y-6=-18-6\)

\(\displaystyle -4y=-24\)   

Now divide both sides by -4 to solve for y;

\(\displaystyle -4y/-4=-24/-4\)

\(\displaystyle {\color{Red} y=6}\)

If you want to check your answers, just plug in your values of x and y into either of the equations. Since they are equations, if both sides are equal, you got the right answers.

There are two ways to solve for x and y in a pair of equations. One way is to add the two equations together, eliminating one of the variables. This may require multiplying one of the equations by a positive or negative number. The other method is to pick one of the equations and solve for one of the variables. Then plug the value you found for the variable into the other equation and solve for a variable. Then you will plug in the solved value for that variable into either equation and solve for the other equation. Remember, you can solve for x and y using either of these methods. This time, let's solve for x then substitute that value into the other equation:

\(\displaystyle 4x+y=31\)

\(\displaystyle x+3y=16\)

Let's solve for x using the bottom equation. It would be easier than to divide the top equation by 4 to solve for x: So let's subtract 3y from each side in order to solve for x:

\(\displaystyle x+3y-3y=16-3y\)

\(\displaystyle x=16-3y\)   

Now just plug this into the other (top) equation to solve for y

\(\displaystyle 4(16-3y)+y=31\)

\(\displaystyle 64-12y+y=31\)

\(\displaystyle 64-11y=31\)   

Now subtract 64 from both sides to isolate y:

\(\displaystyle 64-11y-64=31-64\)

\(\displaystyle -11y=-33\)     

Now divide both sides by -11 to solve for y:

\(\displaystyle {\color{Red} y=3}\)     

Now just plug in the known value of y into either of the equations in order to solve for x. Let's pick the top equation:

\(\displaystyle 4x+(3)=31\)   

Now subtract three from each side:

\(\displaystyle 4x+3-3=31-3\)

\(\displaystyle 4x=28\)             

Now divide both sides by four to solve for x:

\(\displaystyle 4x/4=28/4\)

\(\displaystyle {\color{Red} x=7}\)

If you want to check your answers, plug in both values of x and y into either equation, and since it's an equation, both sides will be equal if your answers are correct.

There are two ways to solve for x and y in a pair of equations. The first method is to add the two equations together, eliminating a variable. This may require multiplying an equation by a positive or negative number in order to eliminate one of the variables. Since there are odd and even numbers in front of the variables in this case, it would be easier to use the second method, which is solving for a variable, then plugging in that value into the other equation. So let's pick the bottom equation to solve for x:

\(\displaystyle 2x+2y=12\)   

Subtract 2y from each side to isolate x:

\(\displaystyle 2x+2y-2y=12-2y\)    

\(\displaystyle 2x=12-2y\)       

Now divide both sides by 2 to solve for x:

\(\displaystyle 2x/2=12/2-2y/2\)

\(\displaystyle x=6-y\)     

Now plug in this value for x into the other (top) equation:

\(\displaystyle 9(6-y)-7y=6\)

\(\displaystyle 54-9y-7y=6\)

\(\displaystyle 54-16y=6\)       

Subtract 54 from each side to isolate y:

\(\displaystyle 54-16y-54=6-54\)

\(\displaystyle -16y=-48\)       

Now divide both sides by -16 to solve for y:

\(\displaystyle -16y/-16=-48/-16\)

\(\displaystyle {\color{Red} y=3}\)     

Now plug in the value of y into either equation to solve for x:

Let's pick the bottom equation:

\(\displaystyle 2x+2(3)=12\)

\(\displaystyle 2x+6=12\)       

Now subtract six from both sides to isolate x:

\(\displaystyle 2x+6-6=12-6\)

\(\displaystyle 2x=6\)                 

Now divide both sides by 2 to solve for x:

\(\displaystyle 2x/2=6/2\)

\(\displaystyle {\color{Red} x=3}\)

You can check your answers by plugging in your answers into either of the equations:  

Since they are equations, if both sides are equal, your answers are correct.

There are 2 ways to solve this set of equations. First, you can solve for one of the variables, then substitute that value for the variable in the other equation. The other way is to add the equations together (combine), and to do this, sometimes multiplying one of the equation by a positive or negative number is required. Let's see how we can do this:  

Remember the key is to add the two equations together and eliminate one of the variables:

In this case, you can see how if you add the two equations together, the y variable is eliminated, since y and -y eliminate each other:

\(\displaystyle 9x+y=22\)

\(\displaystyle 7x-y=10\)     

When you combine the two equations, you get:

\(\displaystyle 16x=32\)         

Divide both sides by 16 to solve for x:

\(\displaystyle 16x/16=32/16\)

\(\displaystyle {\color{Red} x=2}\)               

To solve for y, plug in the value of x into either equation.      

Let's  pick the top equation:

\(\displaystyle 9(2)+y=22\)

\(\displaystyle 18+y=22\)   

Now subtract 18 from each side to solve for y:

\(\displaystyle 18+y-18=22-18\)

\(\displaystyle {\color{Red} y=4}\)

You can check your answers by plugging your answers into either of the two equations. Since it is an equation, both sides will be equal if your answers are correct.

There are 2 ways to solve this set of equations. First, you can solve for one of the variables, then substitute that value for the variable in the other equation. The other way is to add the equations together (combine), and to do this, sometimes multiplying one of the equation by a positive or negative number is required. Let's see how we can do this:  

Remember the key is to add the two equations together and eliminate one of the variables.

In this case, you can see how you can eliminate the y variable by multiplying the bottom equation by 2 so that way 4y and -4y will cancel each other out:

\(\displaystyle (9x-2y=40)2\)

\(\displaystyle 18x-4y=80\)   

\(\displaystyle 3x+4y=46\)

so now adding the top equation and the bottom equation that was multiplied by 2 gives you:

\(\displaystyle 21x=126\)     

Now divide both sides by 21 to solve for x:

\(\displaystyle 21x/21=126/21\)

\(\displaystyle {\color{Red} x=6}\)   

Now pick either equation and plug in the value of x to solve for y:

Let's pick the top equation:

\(\displaystyle 3(6)+4y=46\)

\(\displaystyle 18+4y=46\)   

Now subtract 18 from each side to isolate y:

\(\displaystyle 18+4y-18=46-18\)

\(\displaystyle 4y=28\)           

Now divide both sides by 4 to solve for y:

\(\displaystyle 4y/4=28/4\)

\(\displaystyle {\color{Red} y=7}\)

To check your answers, just plug in your answers into either equation, and since it is an equation, both sides will be equal if your answers are correct.