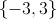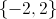We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

College Algebra : Solving Equations and Inequallities

Study concepts, example questions & explanations for College Algebra

Create An Account

All College Algebra Resources

5 Diagnostic Tests 84 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Solving Non Quadratic Polynomials

Give all real solutions of the following equation:

$x^{4} +5x^{2} - 36 = 0$

Possible Answers:

$\left \{ 2,3\right \}$

$\left \{ -3,3\right \}$

$\left \{ -3, -2, 2, 3\right \}$

$\left \{ -3, -2\right \}$

$\left \{ -2,2\right \}$

Correct answer:

$\left \{ -2,2\right \}$

Explanation:

By substituting $u = x^{2}$ - and, subsequently, $u^{2} =\left ( x^{2} \right )^{2} = x^{4}$ this can be rewritten as a quadratic equation, and solved as such:

$x^{4} +5x^{2} - 36 = 0$

$u^{2} + 5u - 36 = 0$

We are looking to factor the quadratic expression as (u+?)(u+?) , replacing the two question marks with integers with product and sum 5; these integers are 9,-4 .

(u+9)(u-4) = 0

Substitute back:

$(x^{2}+9)(x^{2}-4) = 0$

The first factor cannot be factored further. The second factor, however, can itself be factored as the difference of squares:

$(x^{2}+9)(x+2)(x-2) = 0$

Set each factor to zero and solve:

$x^{2}+9= 0$

$x^{2}= -9$

Since no real number squared is equal to a negative number, no real solution presents itself here.

$x-2= 0 \Rightarrow x = 2$

$x+2 = 0 \Rightarrow x = - 2$

The solution set is $\left \{ -2, 2\right \}$ .

Report an Error

Example Question #1 : Solving Equations And Inequallities

Give all real solutions of the following equation:

$x^{4} - 13x^{2} + 36 = 0$

Possible Answers:

$\left \{ -3, -2, 2, 3\right \}$

The equation has no real solutions.

$\left \{ -9,-4,4,9\right \}$

$\left \{ 2, 3\right \}$

$\left \{ 4,9\right \}$

Correct answer:

$\left \{ -3, -2, 2, 3\right \}$

Explanation:

By substituting $u = x^{2}$ - and, subsequently, $u^{2} =\left ( x^{2} \right )^{2} = x^{4}$ this can be rewritten as a quadratic equation, and solved as such:

$x^{4} - 13x^{2} + 36 = 0$

$u^{2} - 13u + 36 = 0$

We are looking to factor the quadratic expression as (u+?)(u+?) , replacing the two question marks with integers with product 36 and sum ; these integers are -9,-4 .

(u-9)(u-4) = 0

Substitute back:

$(x^{2}-9)(x^{2}-4) = 0$

These factors can themselves be factored as the difference of squares:

(x+3)(x-3)(x+2)(x-2) = 0

Set each factor to zero and solve:

$x-3 = 0 \Rightarrow x = 3$

$x-2= 0 \Rightarrow x = 2$

$x+2 = 0 \Rightarrow x = - 2$

$x+3 = 0 \Rightarrow x = - 3$

The solution set is $\left \{ -3, -2, 2, 3\right \}$ .

Report an Error

Example Question #1 : Solve Linear Equations With Rational Number Coefficients: Ccss.Math.Content.8.Ee.C.7b

Solve for :

8x-5-4x=-x+10

Possible Answers:

Correct answer:

Explanation:

8x-5-4x=-x+10 can be simplified to become

4x-5=-x+10

Then, you can further simplify by adding 5 and to both sides to get 5x=15 .

Then, you can divide both sides by 5 to get x=3 .

Report an Error

Example Question #2 : How To Find The Solution To An Equation

Solve for :

6x-1=12x+8-3x

Possible Answers:

Correct answer:

Explanation:

To solve for , you must first combine the 's on the right side of the equation. This will give you $\ 6x-1=9x+8$ .

Then, subtract and from both sides of the equation to get -9=3x .

Finally, divide both sides by to get the solution x=-3 .

Report an Error

Example Question #1 : Solving Equations And Inequallities

Solve the following equation for :

2(x + 5) = -4

Possible Answers:

-4.5

Correct answer:

Explanation:

The first step is to distribute (multiply) the 2 through the parentheses:

2(x+5) = -4

2x + 10 = -4

Then isolate on the left side of the equation. Subtract the 10 from the left and right side.

2x + 10 = -4

2x = -14

Finally, to isolate , divide the left side by 2 so that the 2 cancels out. Then divide by 2 on the right side as well.

2x = -14

x = -7

You can verify this answer by plugging the into the original equation.

Report an Error

Example Question #2 : Solving Equations And Inequallities

Solve for :

6x-3-4x+5=3(x-1)

Possible Answers:

Correct answer:

Explanation:

Combine like terms on the left side of the equation: 2x+2=3(x-1)

Use the distributive property to simplify the right side of the equation: 2x+2=3x-3

Next, move the 's to one side and the integers to the other side: x=5

Report an Error

Example Question #3 : Solving Equations And Inequallities

Solve for x: 12x-5(x-2)=45

Possible Answers:

$x=\frac{7}{55}$

x=5

x=7

x=8

$x=\frac{55}{7}$

Correct answer:

x=5

Explanation:

12x-5(x-2)=45

Simplify the parenthesis:

12x-5x+10=45

Combine the terms with x's:

7x+10=45

Combine constants:

$7x=35\rightarrow \mathbf{x=5}$

Report an Error

Example Question #4 : Solving Equations And Inequallities

Solve the following equation when y is equal to four.

14y-12x=200

Possible Answers:

x=-12

x=144

x=-14

x=12

Correct answer:

x=-12

Explanation:

Solve the following equation when y is equal to four.

14y-12x=200

To solve this equation, we need to plug in 4 for y and solve.

14(4)-12x=200

56-12x=200

-12x=144

x=-12

Report an Error

Example Question #4 : Solving Equations And Inequallities

Solve the following:

3x-7=2

Possible Answers:

x=-3

$x=\frac{-5}{3}$

x=3

$x=\frac{5}{3}$

Correct answer:

x=3

Explanation:

To solve, we must isolate x. In order to do that, we must first add 7 to both sides.

3x-7+7=2+7

3x=9

Next, we must divide both sides by 3.

$\frac{3x}{3}=\frac{9}{3}$

x=3

Report an Error

Example Question #1 : Solving Equations And Inequallities

Write an equation of the line passing through (5,10) and (10,2).

Possible Answers:

$y=\frac{8}{5}x-18$

$y= \frac{8}{5}x+18$

$y=\frac{5}{8}x+9$

None of these.

$y= -\frac{8}{5}x+18$

Correct answer:

$y= -\frac{8}{5}x+18$

Explanation:

To find this line, first find the slope (m) between the two coordinate points. Then use the point-slope formula to find a line with that same slope passing through a particular point.

$m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}= \frac{2-10}{10-5}=-\frac{8}{5}$

$y-y_{1}=m(x-x_{1})$

$y-10=-\frac{8}{5}(x-5) \rightarrow y-10=-\frac{8}{5}x+8 \rightarrow \boldsymbol{y=-\frac{8}{5}x+18}$

Report an Error

View College Algebra Tutors

Priyanka
Certified Tutor

CUNY Hunter College, Bachelor in Arts, Economics.

View College Algebra Tutors

Vince
Certified Tutor

Salt Lake Community College, Associate in Science, Mathematics.

View College Algebra Tutors

Shifrah
Certified Tutor

University of Maryland-Baltimore County, Bachelor of Science, Biology, General. Massachusetts College of Pharmacy and Health ...

All College Algebra Resources

5 Diagnostic Tests 84 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

MCAT Tutors in Seattle, French Tutors in Dallas Fort Worth, GMAT Tutors in New York City, Spanish Tutors in Washington DC, ISEE Tutors in Phoenix, English Tutors in Dallas Fort Worth, ISEE Tutors in Denver, Algebra Tutors in Los Angeles, ISEE Tutors in Atlanta, GRE Tutors in New York City

Popular Courses & Classes

Spanish Courses & Classes in Atlanta, SAT Courses & Classes in Washington DC, LSAT Courses & Classes in Houston, SSAT Courses & Classes in Philadelphia, SSAT Courses & Classes in Houston, Spanish Courses & Classes in Washington DC, GRE Courses & Classes in Boston, ACT Courses & Classes in Boston, ACT Courses & Classes in Los Angeles, MCAT Courses & Classes in Phoenix

Popular Test Prep

MCAT Test Prep in Seattle, GRE Test Prep in Phoenix, ACT Test Prep in Los Angeles, MCAT Test Prep in Atlanta, LSAT Test Prep in Phoenix, MCAT Test Prep in San Francisco-Bay Area, GMAT Test Prep in Denver, SAT Test Prep in Phoenix, ACT Test Prep in Boston, GMAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

College Algebra : Solving Equations and Inequallities

Study concepts, example questions & explanations for College Algebra

All College Algebra Resources

Example Questions

Example Question #1 : Solving Non Quadratic Polynomials

Example Question #1 : Solving Equations And Inequallities

Example Question #1 : Solve Linear Equations With Rational Number Coefficients: Ccss.Math.Content.8.Ee.C.7b

Example Question #2 : How To Find The Solution To An Equation

Example Question #1 : Solving Equations And Inequallities

Example Question #2 : Solving Equations And Inequallities

Example Question #3 : Solving Equations And Inequallities

Example Question #4 : Solving Equations And Inequallities

Example Question #4 : Solving Equations And Inequallities

Example Question #1 : Solving Equations And Inequallities

All College Algebra Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: