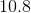All Common Core: 4th Grade Math Resources
Example Questions
Example Question #1 : Use Decimal Notation For Fractions With Denominators 10 Or 100: Ccss.Math.Content.4.Nf.C.6
What decimal is equivalent to 


Example Question #1322 : Numbers And Operations
What decimal is equivalent to 


Example Question #1325 : Numbers And Operations
What decimal is equivalent to 


Example Question #2 : Use Decimal Notation For Fractions With Denominators 10 Or 100: Ccss.Math.Content.4.Nf.C.6
What decimal is equivalent to 


Example Question #1 : Use Decimal Notation For Fractions With Denominators 10 Or 100: Ccss.Math.Content.4.Nf.C.6
Select the decimal that is equivalent to


Example Question #1 : Use Decimal Notation For Fractions With Denominators 10 Or 100: Ccss.Math.Content.4.Nf.C.6
Select the decimal that is equivalent to


Example Question #2 : Use Decimal Notation For Fractions With Denominators 10 Or 100: Ccss.Math.Content.4.Nf.C.6
What decimal is equivalent to 


Example Question #1 : Use Decimal Notation For Fractions With Denominators 10 Or 100: Ccss.Math.Content.4.Nf.C.6
What decimal is equivalent to 


Example Question #3 : Use Decimal Notation For Fractions With Denominators 10 Or 100: Ccss.Math.Content.4.Nf.C.6
What decimal is equivalent to 


Example Question #3 : Use Decimal Notation For Fractions With Denominators 10 Or 100: Ccss.Math.Content.4.Nf.C.6
What decimal is equivalent to 


Certified Tutor
Certified Tutor
All Common Core: 4th Grade Math Resources