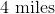All Common Core: 6th Grade Math Resources
Example Questions
Example Question #1 : The Number System
Hydraulic fracturing is a process used by gas companies to rupture and collects pockets of gas trapped within pockets of shale rock. A particular shale fracking site is 

In order to solve this question, we need to first recall how to find the area of a rectangle.
Substitute in the given values in the equation and solve for 
Divide both sides by
Dividing by a fraction is the same as multiplying by its inverse or reciprocal.
Find the reciprocal of
Simplify and rewrite.
Multiply and solve.
Reduce.
The width of the fracking site is
Example Question #2 : The Number System
Hydraulic fracturing is a process used by gas companies to rupture and collects pockets of gas trapped within pockets of shale rock. A particular shale fracking site is 

In order to solve this question, we need to first recall how to find the area of a rectangle.
Substitute in the given values in the equation and solve for 
Divide both sides by
Dividing by a fraction is the same as multiplying by its inverse or reciprocal.
Find the reciprocal of
Simplify and rewrite.
Multiply and solve.
Reduce.
The width of the fracking site is
Example Question #1 : Interpret And Compute Quotients Of Fractions: Ccss.Math.Content.6.Ns.A.1
Hydraulic fracturing is a process used by gas companies to rupture and collects pockets of gas trapped within pockets of shale rock. A particular shale fracking site is 

In order to solve this question, we need to first recall how to find the area of a rectangle.
Substitute in the given values in the equation and solve for 
Divide both sides by
Dividing by a fraction is the same as multiplying by its inverse or reciprocal.
Find the reciprocal of
Simplify and rewrite.
Multiply and solve.
Reduce.
The width of the fracking site is
Example Question #1 : The Number System
Hydraulic fracturing is a process used by gas companies to rupture and collects pockets of gas trapped within pockets of shale rock. A particular shale fracking site is 

In order to solve this question, we need to first recall how to find the area of a rectangle.
Substitute in the given values in the equation and solve for 
Divide both sides by
Dividing by a fraction is the same as multiplying by its inverse or reciprocal.
Find the reciprocal of
Simplify and rewrite.
Multiply and solve.
Reduce.
The width of the fracking site is
Example Question #1 : Interpret And Compute Quotients Of Fractions: Ccss.Math.Content.6.Ns.A.1
Hydraulic fracturing is a process used by gas companies to rupture and collect pockets of gas trapped within pockets of shale rock. A particular shale fracking site is 

In order to solve this question, we need to first recall how to find the area of a rectangle.
Substitute in the given values in the equation and solve for 
Divide both sides by
Dividing by a fraction is the same as multiplying by its inverse or reciprocal.
Find the reciprocal of
Simplify and rewrite.
Multiply and solve.
Reduce.
The width of the fracking site is
Example Question #1 : The Number System
Hydraulic fracturing is a process used by gas companies to rupture and collects pockets of gas trapped within pockets of shale rock. A particular shale fracking site is 

In order to solve this question, we need to first recall how to find the area of a rectangle.
Substitute in the given values in the equation and solve for 
Divide both sides by
Dividing by a fraction is the same as multiplying by its inverse or reciprocal.
Find the reciprocal of
Simplify and rewrite.
Multiply and solve.
Reduce.
The width of the fracking site is
Example Question #1 : Interpret And Compute Quotients Of Fractions: Ccss.Math.Content.6.Ns.A.1
Hydraulic fracturing is a process used by gas companies to rupture and collects pockets of gas trapped within pockets of shale rock. A particular shale fracking site is 

In order to solve this question, we need to first recall how to find the area of a rectangle.
Substitute in the given values in the equation and solve for 
Divide both sides by
Dividing by a fraction is the same as multiplying by its inverse or reciprocal.
Find the reciprocal of
Simplify and rewrite.
Multiply and solve.
Reduce.
The width of the fracking site is
Example Question #2 : Interpret And Compute Quotients Of Fractions: Ccss.Math.Content.6.Ns.A.1
Hydraulic fracturing is a process used by gas companies to rupture and collects pockets of gas trapped within pockets of shale rock. A particular shale fracking site is 

In order to solve this question, we need to first recall how to find the area of a rectangle.
Substitute in the given values in the equation and solve for 
Divide both sides by
Dividing by a fraction is the same as multiplying by its inverse or reciprocal.
Find the reciprocal of
Simplify and rewrite.
Multiply and solve.
The width of the fracking site is
Example Question #1 : The Number System
Hydraulic fracturing is a process used by gas companies to rupture and collects pockets of gas trapped within pockets of shale rock. A particular shale fracking site is 

In order to solve this question, we need to first recall how to find the area of a rectangle.
Substitute in the given values in the equation and solve for 
Divide both sides by
Dividing by a fraction is the same as multiplying by its inverse or reciprocal.
Find the reciprocal of
Simplify and rewrite.
Multiply and solve.
Reduce.
The width of the fracking site is
Example Question #1 : The Number System
Hydraulic fracturing is a process used by gas companies to rupture and collects pockets of gas trapped within pockets of shale rock. A particular shale fracking site is 

In order to solve this question, we need to first recall how to find the area of a rectangle.
Substitute in the given values in the equation and solve for 
Divide both sides by
Dividing by a fraction is the same as multiplying by its inverse or reciprocal.
Find the reciprocal of
Simplify and rewrite.
Multiply and solve.
Reduce.
The width of the fracking site is
All Common Core: 6th Grade Math Resources