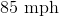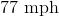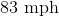All Common Core: 6th Grade Math Resources
Example Questions
Example Question #701 : Ssat Middle Level Quantitative (Math)
A motorcycle travels 

In order to find the motorcyclist’s speed, we need to create a ratio of the miles travelled in a single hour.
Reduce and solve.
Example Question #14 : Ratios & Proportional Relationships
A motorcycle travels 

In order to find the motorcyclist’s speed, we need to create a ratio of the miles travelled in a single hour.
Reduce and solve.
Example Question #41 : Numbers And Operations
A motorcycle travels 

In order to find the motorcyclist’s speed, we need to create a ratio of the miles travelled in a single hour.
Reduce and solve.
Example Question #42 : Numbers And Operations
A motorcycle travels 

In order to find the motorcyclist’s speed, we need to create a ratio of the miles travelled in a single hour.
Reduce and solve.
Example Question #111 : Numbers And Operations
A motorcyclist travels 

In order to find the motorcyclist’s speed, we need to create a ratio of the miles travelled in a single hour.
Reduce and solve.
Example Question #111 : Numbers And Operations
A motorcycle travels 

In order to find the motorcyclist’s speed, we need to create a ratio of the miles travelled in a single hour.
Reduce and solve.
Example Question #11 : Grade 6
A motorcycle travels 

In order to find the motorcyclist’s speed, we need to create a ratio of the miles travelled in a single hour.
Reduce and solve.
Example Question #1 : Understand The Concept Of A Unit Rate: Ccss.Math.Content.6.Rp.A.2
A motorcycle travels 

In order to find the motorcyclist’s speed, we need to create a ratio of the miles travelled in a single hour.
Reduce and solve.
Example Question #21 : Ratios & Proportional Relationships
A motorcycle travels 

In order to find the motorcyclist’s speed, we need to create a ratio of the miles travelled in a single hour.
Reduce and solve.
Example Question #2 : Understand The Concept Of A Unit Rate: Ccss.Math.Content.6.Rp.A.2
A motorcycle travels 

In order to find the motorcyclist’s speed, we need to create a ratio of the miles travelled in a single hour.
Reduce and solve.
All Common Core: 6th Grade Math Resources