GRE Math : How to find out a mixed fraction from an improper fraction
Study concepts, example questions & explanations for GRE Math
All GRE Math Resources
Example Questions
Example Question #1 : How To Find Out A Mixed Fraction From An Improper Fraction
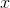
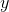
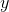
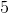
Quantity A:
Quantity B:
The two quantities are equal.
The relationship cannot be determined.
Quantity A is greater.
Quantity B is greater.
The relationship cannot be determined.
Recall that the exponent of the denominator is sutracted from the exponent of the numerator.
Therefore Quantity A is equivalent to x5–y, and because we would then be comparing an arithmetic operation to a geometric operation, it does not matter whether y is a multiple of 5. The two quantities cannot be compared.
Example Question #2 : How To Find Out A Mixed Fraction From An Improper Fraction
Which of the following is the mixed fraction equivalent to 
To begin, notice that using your calculator, you can find:
Now, the closest even multiple of 
This is the same as:
Example Question #3 : How To Find Out A Mixed Fraction From An Improper Fraction
Which of the following is equivalent to 
Although there are many ways to convert improper fractions into mixed fractions, the easiest way is to use your calculator to your advantage. Begin by dividing 
Example Question #2 : How To Find Out A Mixed Fraction From An Improper Fraction
Quantity A:
Quantity B:
Which of the following is true?
The two quantities are equal
Quantity A is larger.
Quantity B is larger.
The relationship of the two quantities cannot be determined based on the information provided.
The two quantities are equal
Though there are several ways you could solve this, let's convert the improper fraction into a mixed one so we can compare them. Start by dividing 
Now, since we know that the two numbers have the same whole-number value, we need to compare their decimal portions. Compare 
All GRE Math Resources
