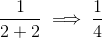We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

GRE Subject Test: Math : Limits

Study concepts, example questions & explanations for GRE Subject Test: Math

Create An Account

All GRE Subject Test: Math Resources

2 Diagnostic Tests 148 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Limits

Evaluate: $\lim_{x \to 2} \frac {x-2}{x^2-4}$

Possible Answers:

$\frac {1}{4}$

$\frac {1}{2}$

$-\frac {1}{4}$

Undefined/No Limit

Correct answer:

$\frac {1}{4}$

Explanation:

Step 1: See if we can plug in x=2 into the equation..

We can't because the denominator becomes ..

Step 2: Factor the denominator:

(x^2-4)=(x-2)(x+2) (By the Difference of Perfect Squares Formula)

Step 3: Re-write the function:

$\frac {(x-2)}{[(x-2)(x+2)]}$

Step 4: Divide by (x-2) on both the numerator and denominator because it's common:

We are left with: $\frac {1}{(x+2)}$

Step 5: Plug in x=2 :

$\frac {1}{2+2}\implies \frac {1}{4}$

The limit of this function as x approaches 2 is $\frac {1}{4}$ .

Report an Error

Example Question #1 : Euler's Method And L'hopital's Rule

Evaluate:

$\lim_{x\rightarrow \infty } \frac{x \sin^{2} x}{2^{x} - 1}$

Possible Answers:

$\frac{1}{2}$

The limit does not exist.

$\infty$

Correct answer:

Explanation:

Let's examine the limit

$\lim_{x\rightarrow \infty } \frac{x }{2^{x} - 1}$

first.

$\lim_{x\rightarrow \infty }x= \lim_{x\rightarrow \infty } \left ( 2^{x} - 1 \right )= \infty$

$\frac{\mathrm{d} }{\mathrm{d} x}x = 1$

and

$\frac{\mathrm{d} }{\mathrm{d} x}\left ( 2^{x} - 1 \right ) = \frac{\mathrm{d} }{\mathrm{d} x}\left ( e^{ x \ln 2} - 1 \right )$

$= \frac{\mathrm{d} }{\mathrm{d} x}e^{ x \ln 2} - \frac{\mathrm{d} }{\mathrm{d} x} 1$

$=\ln 2 \cdot e^{ x \ln 2} - 0 = \ln 2 \cdot 2^{x}$ ,

so by L'Hospital's Rule,

$\lim_{x\rightarrow \infty } \frac{x }{2^{x} - 1} = \lim_{x\rightarrow \infty } \frac{1 }{\ln 2 \cdot 2^{x}}$

Since $\lim_{x\rightarrow \infty } \ln 2 \cdot 2^{x} = \infty$ ,

$\lim_{x\rightarrow \infty } \frac{x }{2^{x} - 1} = \lim_{x\rightarrow \infty } \frac{1 }{\ln 2 \cdot 2^{x}} = 0$

Now, for each x > 0 , $0 \leq \sin^{2} x \leq 1$ ; therefore,

$0 \leq \frac{x \sin^{2} x}{2^{x} - 1} \leq \frac{x }{2^{x} - 1}$

By the Squeeze Theorem,

$0 \leq \lim_{x\rightarrow \infty } \frac{x \sin^{2} x}{2^{x} - 1} \leq \lim_{x\rightarrow \infty } \frac{x }{2^{x} - 1} = 0$

and

$\lim_{x\rightarrow \infty } \frac{x \sin^{2} x}{2^{x} - 1} = 0$

Report an Error

Example Question #2 : Euler's Method And L'hopital's Rule

Evaluate:

$\lim_{x\rightarrow \infty } \frac{5^{x} - 1}{3^{x} - 1}$

Possible Answers:

The limit does not exist.

$\ln \frac{5}{3}$

$\frac{\ln 5}{\ln 3}$

$\infty$

$\frac{5}{3}$

Correct answer:

$\infty$

Explanation:

$\lim_{x\rightarrow \infty }\left ( 5^{x} - 1 \right ) = \lim_{x\rightarrow \infty }\left ( 3^{x} - 1 \right ) = \infty$

Therefore, by L'Hospital's Rule, we can find $\lim_{x\rightarrow \infty } \frac{5^{x} - 1}{3^{x} - 1}$ by taking the derivatives of the expressions in both the numerator and the denominator:

$\frac{\mathrm{d} }{\mathrm{d} x}\left ( 5^{x} - 1 \right ) = \frac{\mathrm{d} }{\mathrm{d} x}\left ( e^{x \ln 5} - 1 \right )$

$= \frac{\mathrm{d} }{\mathrm{d} x} e^{x \ln 5 } - \frac{\mathrm{d} }{\mathrm{d} x}1$

$=\ln 5\cdot e^{x \ln 5 } - 0 = \ln 5\cdot 5^{x }$

Similarly,

$\frac{\mathrm{d} }{\mathrm{d} x}\left ( 3^{x} - 1 \right ) = \ln 3 \cdot 3 ^{x}$

$\lim_{x\rightarrow \infty } \frac{5^{x} - 1}{3^{x} - 1} = \lim_{x\rightarrow \infty } \frac{\ln 5 \cdot 5^{x} }{\ln 3 \cdot 3^{x} }$

$=\frac{\ln 5 }{\ln 3 } \cdot \lim_{x\rightarrow \infty } \frac{ 5^{x} }{ 3^{x} }= \frac{\ln 5 }{\ln 3 } \cdot \lim_{x\rightarrow \infty }\left ( \frac{ 5 }{ 3 } \right )^{x}$

But $\lim_{x\rightarrow \infty }a^{x} = \infty$ for any a > 1 , so

$\lim_{x\rightarrow \infty } \frac{5^{x} - 1}{3^{x} - 1}= \frac{\ln 5 }{\ln 3 } \cdot \lim_{x\rightarrow \infty }\left ( \frac{ 5 }{ 3 } \right )^{x} = \infty$

Report an Error

Example Question #3 : Euler's Method And L'hopital's Rule

Evaluate:

$\lim_{x\rightarrow 0 } \frac{7^{x} - 1}{2^{x} - 1}$

Possible Answers:

$\log_{2}7$

$\infty$

$\ln \frac{7}{2}$

$\frac{1}{2}\ln 7$

The limit does not exist.

Correct answer:

$\log_{2}7$

Explanation:

$\lim_{x\rightarrow 0 }\left ( 7^{x} - 1 \right ) = 7^{0} - 1 = 1- 1 = 0$

and

$\lim_{x\rightarrow 0 }\left ( 2^{x} - 1 \right ) = 2^{0} - 1 = 1- 1 = 0$

Therefore, by L'Hospital's Rule, we can find $\lim_{x\rightarrow 0 } \frac{7^{x} - 1}{2^{x} - 1}$ by taking the derivatives of the expressions in both the numerator and the denominator:

$\frac{\mathrm{d} }{\mathrm{d} x}\left ( 7^{x} - 1 \right ) = \frac{\mathrm{d} }{\mathrm{d} x}\left ( e^{x \ln 7} - 1 \right )$

$= \frac{\mathrm{d} }{\mathrm{d} x} e^{x \ln 7 } - \frac{\mathrm{d} }{\mathrm{d} x}1$

$=\ln 7\cdot e^{x \ln 7 } - 0 = \ln 7\cdot 7^{x }$

Similarly,

$\frac{\mathrm{d} }{\mathrm{d} x}\left ( 2^{x} - 1 \right ) = \ln 2 \cdot 2 ^{x}$

$\lim_{x\rightarrow 0 } \frac{7^{x} - 1}{2^{x} - 1} = \lim_{x\rightarrow 0 } \frac{ \ln 7\cdot 7^{x }}{ \ln 2\cdot 2^{x }}$

$= \frac{ \ln 7 \cdot 7^{0 }}{ \ln 2\cdot 2^{0 }} = \frac{ \ln 7\cdot 1}{ \ln 2\cdot 1} = \frac{ \ln 7}{ \ln 2 }= \log_{2}7$

Report an Error

Example Question #4 : Euler's Method And L'hopital's Rule

Evaluate:

$\lim_{x\rightarrow 0^{+} } \frac{x \sin x}{2^{x} - 1}$

Possible Answers:

$\ln 2$

$\frac{1}{\ln2}$

Correct answer:

Explanation:

$\lim_{x\rightarrow 0^{+} } x \sin x= 0 \cdot \sin 0 = 0$

and

$\lim_{x\rightarrow 0^{+} } \left ( 2 ^{x} - 1 \right )= 2^{0} -1 = 0$

Therefore, by L'Hospital's Rule, we can find $\lim_{x\rightarrow 0^{+} } \frac{x \sin x}{2^{x} - 1}$ by taking the derivatives of the expressions in both the numerator and the denominator:

$\frac{\mathrm{d} }{\mathrm{d} x}x \sin x = \frac{\mathrm{d} }{\mathrm{d} x} x \cdot \sin x + \frac{\mathrm{d} }{\mathrm{d} x}\sin x \cdot x$

$= 1 \cdot \sin x + \cos x \cdot x = \sin x + x \cos x$

$\frac{\mathrm{d} }{\mathrm{d} x}\left ( 2^{x} - 1 \right ) = \frac{\mathrm{d} }{\mathrm{d} x}\left ( e^{x \ln 2} - 1 \right )$

$= \frac{\mathrm{d} }{\mathrm{d} x} e^{x \ln 2} - \frac{\mathrm{d} }{\mathrm{d} x} 1$

$= \ln 2\cdot e^{x \ln 2} - 0 = \ln 2\cdot 2^{x }$

$\lim_{x\rightarrow 0^{+} } \frac{x \sin x}{2^{x} - 1} = \lim_{x\rightarrow 0^{+} } \frac{\sin x + x \cos x}{ \ln 2\cdot 2^{x }}$

$= \frac{\sin 0 + 0 \cos 0}{ \ln 2\cdot 2^{0 }} = \frac{ 0 + 0 }{ \ln 2\cdot 1} = 0$

Report an Error

Example Question #1 : L'hospital's Rule

Solve:

${}\lim_{x \to \infty} x^\frac{5}{x}}$

Possible Answers:

e^5

ln(5)

Correct answer:

Explanation:

Substitution is invalid. In order to solve ${}{ \lim_{x \to \infty} x^\frac{5}{x}}$ , rewrite this as an equation.

${} y= { \lim_{x \to \infty} x^\frac{5}{x}}$

Take the natural log of both sides to bring down the exponent.

${} \lim_{x \to \infty} ln(y)= \lim_{x \to \infty} \frac{5}{x} \cdot ln(x)$

${} \lim_{x \to \infty} ln(y)= 5\lim_{x \to \infty} \frac{ln(x)}{x}$

Since ${} \lim_{x \to \infty} \frac{ln(x)}{x}$ is in indeterminate form, ${}\frac{\infty}{\infty}$ , use the L'Hopital Rule.

L'Hopital Rule is as follows:

$\lim_{x\rightarrow \infty} \frac{f(x)}{g(x)}=\lim_{x\rightarrow \infty}\frac{f'(x)}{g'(x)}$

${} \lim_{x \to \infty} \frac{ln(x)}{x} = \lim_{x \to \infty} \frac{\frac{1}{x}}{1} = 0$

This indicates that the right hand side of the equation is zero.

${} \lim_{x \to \infty} ln(y)= 0$

Use the term to eliminate the natural log.

${} \lim_{x \to \infty} e^l^n^(^y^)= e^0$

$\lim_{x \to \infty} y=e^0=1$

Report an Error

Example Question #1 : L'hospital's Rule

Evaluate the limit using L'Hopital's Rule.

$\lim_{x\rightarrow \infty }\frac{x^2}{e^x+1}$

Possible Answers:

Undefined

$\infty$

Correct answer:

Explanation:

L'Hopital's Rule is used to evaluate complicated limits. The rule has you take the derivative of both the numerator and denominator individually to simplify the function. In the given function we take the derivatives the first time and get

$\lim_{x\rightarrow \infty }\frac{2x}{e^x}$ .

This still cannot be evaluated properly, so we will take the derivative of both the top and bottom individually again. This time we get

$\lim_{x\rightarrow \infty }\frac{2}{e^x}$ .

Now we have only one x, so we can evaluate when x is infinity. Plug in infinity for x and we get

$\frac{2}{e^\infty }$ and $e^\infty=\infty$ .

So we can simplify the function by remembering that any number divided by infinity gives you zero.

Report an Error

Example Question #1 : L'hospital's Rule

Evaluate the limit using L'Hopital's Rule.

$\lim_{x \to 0} \frac{2x^2}{ln(x)}$

Possible Answers:

$\infty$

Undefined

Correct answer:

Explanation:

$\lim_{x\rightarrow 0}\frac{4x}{\frac{1}{x}}=\lim_{x\rightarrow 0}4x^2$ .

Since the first set of derivatives eliminates an x term, we can plug in zero for the x term that remains. We do this because the limit approaches zero.

This gives us

$4\cdot 0^2=0$ .

Report an Error

Example Question #2 : L'hospital's Rule

Evaluate the limit using L'Hopital's Rule.

$\lim_{x\rightarrow \infty }\frac{5x^3+1}{3x^2}$

Possible Answers:

$\frac{15}{6}$

$\frac{5}{3}$

$\infty$

Undefined

Correct answer:

$\infty$

Explanation:

$\lim_{x\rightarrow \infty }\frac{15x^2}{6x}$ .

This still cannot be evaluated properly, so we will take the derivative of both the top and bottom individually again. This time we get

$\lim_{x\rightarrow \infty }\frac{30x}{6}=5x$ .

Now we have only one x, so we can evaluate when x is infinity. Plug in infinity for x and we get

$5\cdot \infty=\infty$ .

Report an Error

Example Question #3 : L'hospital's Rule

Calculate the following limit.

$\lim_{x\rightarrow2} \frac{x^2-4}{2x-4}$

Possible Answers:

Correct answer:

Explanation:

To calculate the limit, often times we can just plug in the limit value into the expression. However, in this case if we were to do that we get $\frac00$ , which is undefined.

What we can do to fix this is use L'Hopital's rule, which says

$\lim_{x\rightarrow 2} \frac{f(x)}{g(x)}=\lim_{x\rightarrow 2} \frac{f'(x)}{g'(x)}$ .

So, L'Hopital's rule allows us to take the derivative of both the top and the bottom and still obtain the same limit.

$\lim_{x-\rightarrow 2} \frac{x^2-4}{2x-4}=\lim_{x\rightarrow 2} \frac{2x}{2}$ .

Plug in x=2 to get an answer of .

Report an Error

View Tutors

Abdul Azeez
Certified Tutor

University of Manitoba, Master's/Graduate, Business.

View Tutors

Evgenii
Certified Tutor

View Tutors

Omar
Certified Tutor

Arizona State University, Bachelors, Civil Engineering.

All GRE Subject Test: Math Resources

2 Diagnostic Tests 148 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Spanish Tutors in San Francisco-Bay Area, Algebra Tutors in Chicago, GMAT Tutors in Philadelphia, SAT Tutors in Philadelphia, Physics Tutors in Los Angeles, Computer Science Tutors in Atlanta, Reading Tutors in Dallas Fort Worth, ISEE Tutors in Seattle, SAT Tutors in San Diego, English Tutors in San Diego

Popular Courses & Classes

ISEE Courses & Classes in Atlanta, GRE Courses & Classes in Miami, ISEE Courses & Classes in Houston, SSAT Courses & Classes in Boston, SSAT Courses & Classes in New York City, GMAT Courses & Classes in Seattle, ACT Courses & Classes in San Francisco-Bay Area, GMAT Courses & Classes in Boston, ISEE Courses & Classes in Seattle, SAT Courses & Classes in Washington DC

Popular Test Prep

ISEE Test Prep in Denver, ISEE Test Prep in San Francisco-Bay Area, GMAT Test Prep in Philadelphia, GMAT Test Prep in San Francisco-Bay Area, SSAT Test Prep in New York City, SSAT Test Prep in Philadelphia, MCAT Test Prep in Atlanta, ACT Test Prep in Boston, ACT Test Prep in Washington DC, GMAT Test Prep in Boston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

GRE Subject Test: Math : Limits

Study concepts, example questions & explanations for GRE Subject Test: Math

All GRE Subject Test: Math Resources

Example Questions

Example Question #1 : Limits

Example Question #1 : Euler's Method And L'hopital's Rule

Example Question #2 : Euler's Method And L'hopital's Rule

Example Question #3 : Euler's Method And L'hopital's Rule

Example Question #4 : Euler's Method And L'hopital's Rule

Example Question #1 : L'hospital's Rule

Example Question #1 : L'hospital's Rule

Example Question #1 : L'hospital's Rule

Example Question #2 : L'hospital's Rule

Example Question #3 : L'hospital's Rule

All GRE Subject Test: Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: