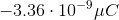Call Now to Set Up Tutoring:

(888) 888-0446

High School Chemistry : Using Avogadro's Number

Study concepts, example questions & explanations for High School Chemistry

Create An Account

All High School Chemistry Resources

6 Diagnostic Tests 143 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Using Avogadro's Number

How many atoms are in $\small 50g$ of calcium?

Possible Answers:

$7.5*10^{23} atoms$

$5.0*10^{24} atoms$

$3.0*10^{25}atoms$

$6.0*10^{23}atoms$

Correct answer:

$7.5*10^{23} atoms$

Explanation:

In order to determine how many atoms are in this sample, we need to convert this sample into moles. Calcium has a molar mass of $\small 40.08$ grams per mole.

$50g\ Ca*\frac{1mol\ Ca}{40.08g\ Ca}=1.25mol\ Ca$

Avogadro's number tells us that there $6.022*10^{23}$ atoms in one mole of any element. We can use this conversion to find the total number of atoms in the sample.

$1.25 moles* \frac{6.022*10^{23}atoms}{1mol} = 7.5*10^{23} atoms$

Report an Error

Example Question #1 : Using Avogadro's Number

How many atoms are there in 47.5g of boron?

Possible Answers:

$2.65*10^{23} \text{atoms}$

$5.15*10^{24} \text{atoms}$

$2.65*10^{24} \text{atoms}$

$3.65*10^{22} \text{atoms}$

Correct answer:

$2.65*10^{24} \text{atoms}$

Explanation:

To do this problem we have to first convert grams to moles, then moles to atoms using Avogadro's number:

$47.5g*\frac{1mol\ B}{10.8g\ B}*\frac{6.022*10^{23}\ \text{atoms}}{1mol}=2.65*10^{24}\text{atoms}$

Report an Error

Example Question #2 : Using Avogadro's Number

How many moles of carbon are in a sample of $25.125*10^{27}$ atoms?

Possible Answers:

$1.51*10^{6} mol$

$4.17*10^{3} mol$

$1.51*10^{4} mol$

$4.17*10^{4} mol$

Correct answer:

$4.17*10^{4} mol$

Explanation:

To solve, we need to convert atoms to moles using Avogadro's number:

$25.125*10^{27}\text{atoms}*\frac{1mol}{6.022*10^{23}\text{atoms}}=4.17*10^4mol$

Report an Error

Example Question #11 : High School Chemistry

How many atoms of sodium are in three moles of $Na_{2}S$ ?

Possible Answers:

$3.61*10^{24} \text{atoms Na}$

$3.61*10^{26} \text{atoms Na}$

$1.31*10^{24} \text{atoms Na}$

$3.61*10^{22} \text{atoms Na}$

Correct answer:

$3.61*10^{24} \text{atoms Na}$

Explanation:

To answer this question, we have to find the number of moles of sodium in this compound. Note that there are two sodium atoms per molecule. Then, multiply the total moles of sodium by Avogadro's number.

$3 mol\ Na_{2}S*\frac{2mol\ Na}{1 mol\ Na_{2}S}*\frac{6.022*10^{23}\text{atoms\ Na}}{1 mole\ Na}=3.61*10^{24}\text{atoms Na}$

Report an Error

Example Question #1 : Using Avogadro's Number

You have a neutral balloon. If you were to add 21,000 electrons to it, what would its net charge be?

$e=1.6\cdot 10^{-19}$ = charge of one electron

Possible Answers:

None of the other answers is correct

$3.36\cdot 10^{-9}\mu C$

$3.08\cdot 10^{-9}\mu C$

$-3.08\cdot 10^{-9}\mu C$

$-3.36\cdot 10^{-9}\mu C$

Correct answer:

$-3.36\cdot 10^{-9}\mu C$

Explanation:

The elemental charge is the magnitude of charge, in Coulombs, that each electron or proton has. Because electrons have a negative charge, don't forget to add a negative sign into the equation.

$q=-(\#\ of\ electrons)(e)$

$q= -(21000)(1.6\cdot 10^{-19})$

$q= -3.36\cdot 10^{-15}$

When you convert the answer to microcoulombs, the answer is $-3.36\cdot 10^{-9}\mu C$ :

$-3.36\cdot 10^{-15} C\cdot\frac{1.0\cdot10^6 \mu C}{1 C}= -3.36\cdot 10^{-9}\mu C$

Report an Error

Example Question #1 : Moles And Molar Mass

What is the mass of $5.34\times10^{15}$ particles of $C_2H_6$ ?

Possible Answers:

$1.78\times 10^{-15}\hspace{1 mm}g\hspace{1 mm}C_2H_6$

$2.66\times 10^{-15}\hspace{1 mm}g\hspace{1 mm}C_2H_6$

$1.78\times 10^{-7}\hspace{1 mm}g\hspace{1 mm}C_2H_6$

$6.02\times 10^{-7}g\hspace{1 mm}C_2H_6$

$2.66\times 10^{-7}g\hspace{1 mm}C_2H_6$

Correct answer:

$2.66\times 10^{-7}g\hspace{1 mm}C_2H_6$

Explanation:

$5.34\times10^{15}\hspace{1 mm}particles\hspace{1 mm}C_2H_6\times \frac{1\hspace{1 mm}mole\hspace{1 mm}C_2H_6}{6.022\times 10^{23}\hspace{1 mm}particles\hspace{1 mm} C_2H_6}\times \frac{30.0\hspace{1 mm}g\hspace{1 mm}C_2H_60=}{1\hspace{1 mm}mole\hspace{1 mm}C_2H_6}=2.66\times 10^{-7}g\hspace{1 mm}C_2H_6$

Report an Error

Example Question #1 : Moles And Molar Mass

How many atoms are in 1 mole of H₂?

Possible Answers:

None of the other answers

6.022 * 10²³

1.2044 * 10²⁴

3.626 * 10⁴⁷

6.022 * 10⁴⁶

Correct answer:

1.2044 * 10²⁴

Explanation:

This question requires an understanding of what avogadro's number actually represents. Avogadro's number, 6.022 * 10²³ is the number of things in one mole. The question indicates that there is 1 mole of H₂. Thus there are 6.022 * 10²³ molecules of H₂. However the question is asking for the amount of atoms in 1 mole of H₂. Thus we must consider the makeup of an H₂ molecule, where we see that it is a diatomic molecule. Thus we must multiply 6.022 * 10²³by 2 to calculate the number of individual atoms present in 1 mole of H₂. We find our answer to be 1.2044 * 10²⁴.

Report an Error

Example Question #3 : Moles And Molar Mass

A chemist has $4.37*10^{-3}g$ of $CH_3CH_2OH$ .

How many molecules of $CH_3CH_2OH$ does she have?

Possible Answers:

$5.72*10^{19}$

$5.72*10^{18}$

$5.73*10^{19}$

$9.50*10^{19}$

$4.73*10^{19}$

Correct answer:

$5.72*10^{19}$

Explanation:

$4.37\times 10^{-3}g\hspace{1 mm}CH_3CH_2OH\times \frac{1\hspace{1 mm}mole\hspace{1 mm}CH_3CH_2OH}{46\hspace{1 mm}g\hspace{1 mm}CH_3CH_2OH}\times\frac{6.022\times 10^{23}\hspace{1 mm}molecules\hspace{1 mm} CH_3CH_2OH}{1\hspace{1 mm}mole\hspace{1 mm}CH_3CH_2OH}=5.72\times10^{19}\hspace{1 mm}molecules\hspace{1 mm}CH_3CH_2OH$

Report an Error

Example Question #4 : Moles And Molar Mass

How many hydrogen atoms are in 46.3 g of ethanol, CH_6O ?

Possible Answers:

$6.0*10^{23}\ \text{atoms}$

$3.1*10^{24}\ \text{atoms}$

$2.7*10^{25}\ \text{atoms}$

$4.9*10^{24}\ \text{atoms}$

Correct answer:

$4.9*10^{24}\ \text{atoms}$

Explanation:

To determine the number of hydrogen atoms, divide the mass of ethanol by its molar mass to get moles of ethanol.

$MM=(12)+6(1)+(16)=34\frac{g}{mol}$

$46.3g*\frac{1mol}{34g}=1.36mol\ CH_6O$

Multiply this by six atoms of hydrogen per molecule of ethanol and by Avogadro's number to get the number of hydrogen atoms.

$1.36mol\ CH_6O*\frac{6mol\ H}{1mol\ CH_6O}=8.17mol\ H$

$8.17mol\ H*\frac{6.022*10^{23}\text{atoms}}{1mol}=4.9*10^{24}\text{atoms}$

Report an Error

Example Question #5 : Moles And Molar Mass

How many hydrogen atoms are present in 500 mL of water at room temperature?

$\rho_{\text{water}}=1\frac{g}{mL}$

Possible Answers:

$5.96*10^{26}\ \text{atoms}$

$1.67*10^{25}\ \text{atoms}$

$3.35*10^{25}\ \text{atoms}$

$5.01*10^{25}\ \text{atoms}$

Correct answer:

$3.35*10^{25}\ \text{atoms}$

Explanation:

Use the density of water, the molar mass of water, and Avogadro's number to calculate the number of molecules of water.

We have 500mL of water. Use the density to convert this to grams; then use the molar mass of water to convert this to moles.

$500mL*\frac{1g}{1mL}*\frac{1mol}{18g}=27.78mol\ H_2O$

There are two moles of hydrogen atoms per one mole of water.

$27.78mol\ H_2O*\frac{2mol\ H}{1mol\ H_2O}=55.56mol\ H$

Finally, multiply by Avogadro's number.

$55.56mol\ H*\frac{6.022*10^{23}\text{atoms}}{1mol}=3.35*10^{25}\text{atoms}$

Report an Error

View Tutors

Andrew
Certified Tutor

The University of Kansas, Bachelor of Science, Biochemistry.

View Tutors

Mr. Henderson
Certified Tutor

Swarthmore College, Bachelor of Science, Engineering. MBU, Master of Science, Education.

View Tutors

Kevin
Certified Tutor

CUNY Hunter College, Bachelors, Biochemistry.

All High School Chemistry Resources

6 Diagnostic Tests 143 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ACT Tutors in Chicago, MCAT Tutors in Denver, Math Tutors in San Diego, Computer Science Tutors in Denver, Biology Tutors in Phoenix, SAT Tutors in Boston, Computer Science Tutors in Chicago, ISEE Tutors in Seattle, Physics Tutors in Phoenix, Calculus Tutors in Philadelphia

Popular Courses & Classes

SAT Courses & Classes in Atlanta, SAT Courses & Classes in Denver, Spanish Courses & Classes in Seattle, ACT Courses & Classes in Phoenix, Spanish Courses & Classes in Houston, GMAT Courses & Classes in Denver, Spanish Courses & Classes in Los Angeles, GRE Courses & Classes in Los Angeles, GRE Courses & Classes in Denver, SSAT Courses & Classes in Philadelphia

Popular Test Prep

ISEE Test Prep in Denver, GMAT Test Prep in New York City, SAT Test Prep in Miami, ISEE Test Prep in Atlanta, ACT Test Prep in Dallas Fort Worth, MCAT Test Prep in Boston, GRE Test Prep in Los Angeles, GMAT Test Prep in Denver, ACT Test Prep in San Diego, LSAT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Chemistry : Using Avogadro's Number

Study concepts, example questions & explanations for High School Chemistry

All High School Chemistry Resources

Example Questions

Example Question #1 : Using Avogadro's Number

Example Question #1 : Using Avogadro's Number

Example Question #2 : Using Avogadro's Number

Example Question #11 : High School Chemistry

Example Question #1 : Using Avogadro's Number

Example Question #1 : Moles And Molar Mass

Example Question #1 : Moles And Molar Mass

Example Question #3 : Moles And Molar Mass

Example Question #4 : Moles And Molar Mass

Example Question #5 : Moles And Molar Mass

All High School Chemistry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: